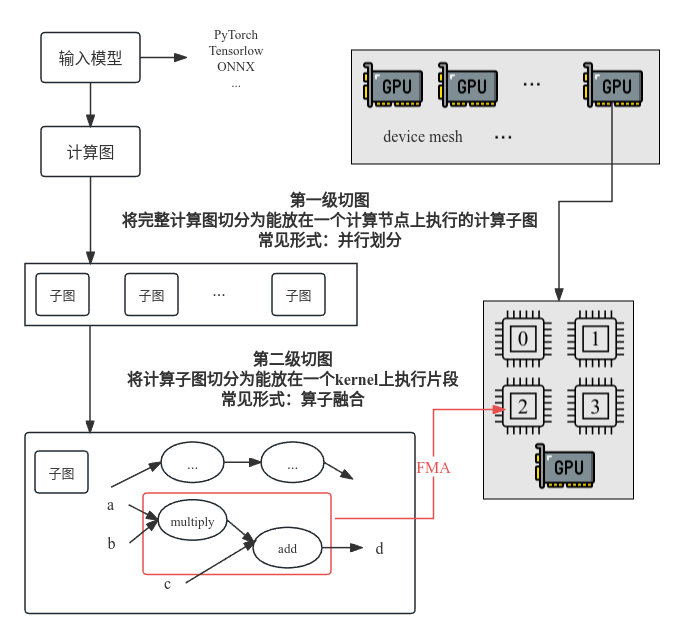
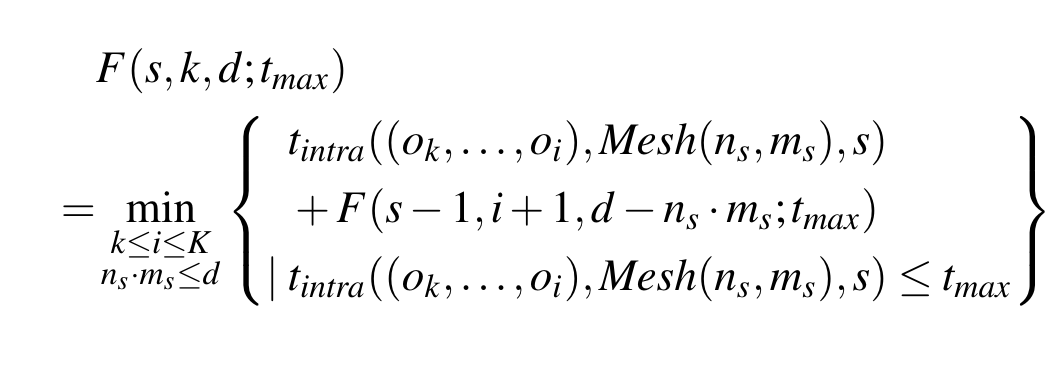Home AI Compiler 中的Auto-Parallelism
Post
Cancel

AI Compiler 中的Auto-Parallelism

Posted Apr 9, 2024 Updated Sep 6, 2024
By tfruan
38 min read

AI编译器可以涉及的两种切图：

（1）为了设备分布式执行切图，将计算图（静态图）切为子图， 为了在内存受限的独立设备上执行

例如：FlexFlow、Alpa

（2）为了launch kernel切图(算子融合)，子图对于硬件kernel可能过大，无法融合为1个kernel，为了便于在auto-scheduler时直接融（tile）为一个kernel，故将将子图切为适应硬件kernel大小的片段

例如：[ISCA ‘23]Inter-layer Scheduling Space Definition and Exploration for Tiled Accelerators，使用资源分配树，来表示不同的层间调度方案，并描述层间调度的整体空间，是将传统的分布式技术从device之间的调度扩展到kernel之间的调度

distribute system.png

本文主要介绍第一种切图

当前痛点：

  • 手工设置分布式策略一般需要逐op或layer，依赖expert experience —> 合理划分任务粒度，设计自动并行策略
  • 设置的自动策略约束关系较多，或者覆盖并行方法（搜索空间）较少 —> 覆盖多种并行方法以及考虑device的分配
  • 自动搜索算法耗时较长，且耗费硬件资源来衡量 —> 设计优秀的模拟器，例如增量衡量并行策略的优异（FlexFlow）
  • 局限于静态图（当前图优化基本都需要静态图）、静态shape（张量并行时需要） —> 对于动态图，提前获得几个可能的静态图，利用这些静态图的最优策略来指导动态图选择并行策略

一些background：

  1. HLO IR

一组正交的primitive operators，其他op都可以由基础op组合表示；只支持静态shape

  1. 分布式

分布式技术：拆分任务（数据+模型），交给多个设备运行

为什么需要：单设备资源限制（算力墙 + 存储墙） + 提升单个设备的成本过高

分布式实现框架：参数服务器 和 集合通信

通信方式：同步通信 和 异步通信

并行方法：

  • 数据并行
  • 模型并行
    • 算子内并行：即张量并行，可以横向/纵向切分
    • 算子间并行
  • 流水并行：可以认为是算子间并行的一种特殊情况（每次只执行一个micro-batch）
  • 混合并行：可以看看DeepSpeed

(下表截取自：https://github.com/ConnollyLeon/awesome-Auto-Parallelism)

NameDescriptionOrganization or authorPaperFrameworkYearAuto Methods
FlexFlowA deep learning framework that accelerates distributed DNN training by automatically searching for efficient parallelization strategiesZhihao Jiahttps://arxiv.org/abs/1807.05358FlexFlow, compatible with PyTorch, Keras2019MCMC search algorithm
Auto-MAPIt works on HLO IR. Use Linkage Group to prune search space Use DQN RL to search DD, MP, PP stategies.Alibabahttps://arxiv.org/abs/2007.04069RAINBOW DQN2020Reinforce Learning
GSPMDA system that uses simple tensor sharding annotations to achieve different parallelism paradigms in a unified wayGooglehttps://arxiv.org/abs/2105.04663Tensorflow XLA2021sharding propagation
AlpaAutomating Inter- and Intra-Operator Parallelism for Distributed Deep LearningUC Berkley, Google, etc.https://arxiv.org/abs/2201.12023Jax, XLA2022Integer Linear for Intra, Dynamic programming for inter
TePDistIt works on HLO IR. Given hierarchical disassembly of the search space of the SPMD strategy.Alibabahttps://arxiv.org/abs/2302.08141Tensorflow XLA2023three levels of granularity: cone(DP), segment(ILP), graph(DP) pipeline stage: ILP

FlexFlow

paper： Beyond Data and Model Parallelism for Deep Neural Networks

repo： https://github.com/flexflow/FlexFlow/tree/inference

概述

  • 区别于传统的data parallel 、model parallel（本文没涉及pipeline paralle）的划分维度，FlexFlow将并行策略的划分维度分为SOAP(Sample-Operation-Attribute-Parameter)
    • Sample: 输入样本的batch_size
    • Operation: op之间的划分维度，算子间并行
    • Attribute: tensor的属性维度（除parameter之外的维度），即height和width
    • Parameter: tensor的parameter维，即channel_in和channel_out
  • FlexFlow引入了execution simulator，使用较少的资源衡量且更快地当前并行策略
    • 使用MCMC搜索算法探索SOAP的空间
    • 对新策略采用增量计算来评估性能

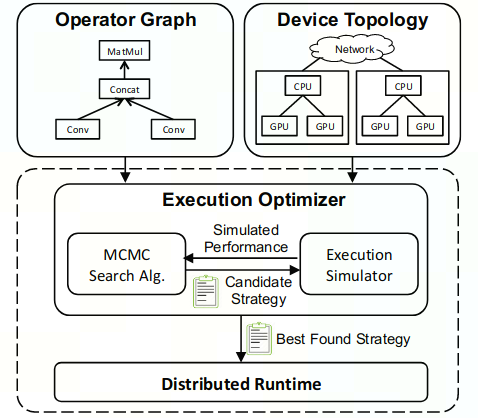
Architecture

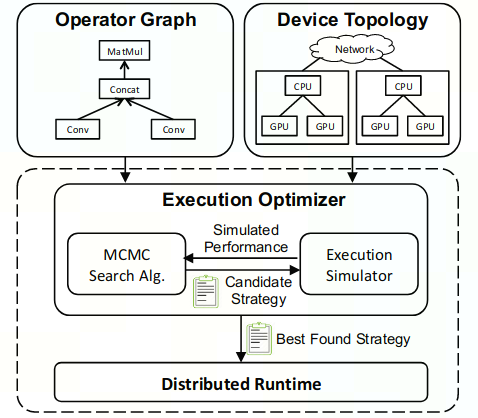
  • 输入：Opeartor Graph和Device Topology
    • Opeartor Graph：输入模型的计算图描述
    • Device Topology：device为节点，设备之间的连接关系（NVLink、PCI-e）为边 不同连接→不同带宽、延迟→适用于不同并行策略
  • 获得最优并行策略：Execution Optimizer
    • MCMC Search Algorithm：基于先前的candidates，迭代地给出新的candidate strategies
    • Execution Sinulator：衡量当前candidate strategy的性能，避免e2e运行
  • Distribute Runtime：资源调度与执行

exe

SOPA

由Sample-Operation-Attribute-Parameter四个可切分维度定义的Search Space

  • Sample: 输入样本的batch_size
  • Operation: op之间的划分维度，算子间并行
  • Attribute: tensor的属性维度（除parameter之外的维度），即height和width
  • Parameter: tensor的parameter维，即in_channel和out_channel

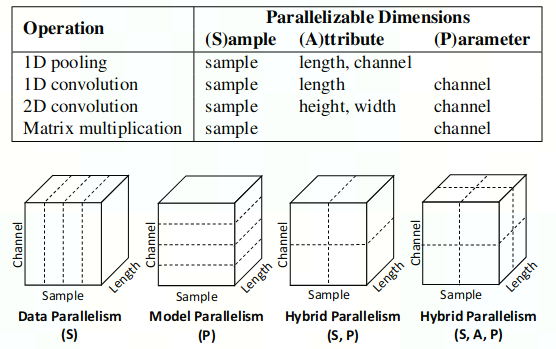
对于每个op都有一组可并行维度，其中包含sample维和其他维。其他维中，如果对该维度进行划分需要对模型参数进行拆分，则为parameter维；反之为attribute维。

下图是一些op的可并行维度

并行维度

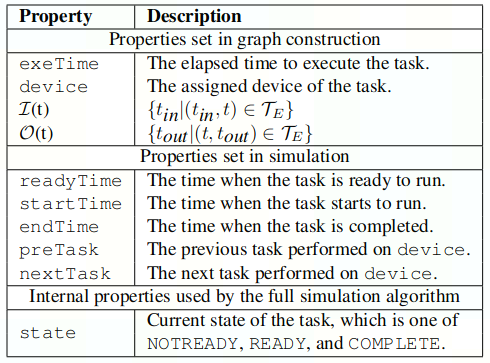
FlexFlow的并行策略S包含了每个op的并行策略

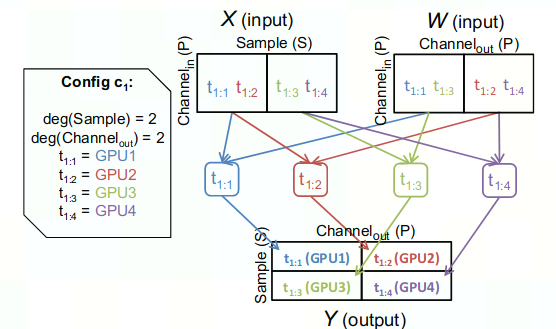
记某个op的并行策略为config c_i ，包含对op的维度切分行为以及执行设备分配如下图左侧，

  • deg(Sample) = 2表示将该op的Sample维度划分为2等份，deg(Channel_out)=2表示将该op的Channel_out维度划分为2等份
  • t_{i}:{k}的值 表示config c_i中，执行任务 t_{i}:{k} 的设备

切分行为以及执行设备分配

Execution Simulator

对给定的candidate strategy模拟执行以评估性能。

假设：

  • 每个op的execution time是predicable并且于独立于输入
    • 用于增量计算。在衡量strategy时，若某个op的input_size和上次执行相同，则直接使用上次执行中的op耗时。在大多数模型中，这个假设成立
  • 设备之间的通信带宽被充分利用
  • runtime的调度开销忽略不计

1.构建task graph

  • 节点：task
    • normal task：op的计算 t_{i}:{k}
    • communication task：设备之间的数据传输 t_c （Alpa中考虑了一个resharding开销，当一个op的input_tensor并不满足该op的切分config时，需要引入额外的resharding开销）
    • 每个task包含以下属性

task graph

  • 边：task之间的先后关系

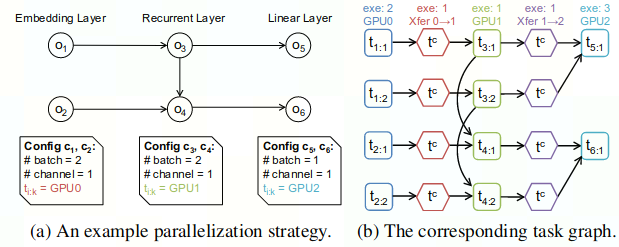
下图是简易网络构建的task graph例

task graph

2.simulator algorithm

规划task graph中任务的执行。使用优先队列保存ready（所有依赖task已经完成且到start_time）状态的task，FIFO执行

(1) full simulator algorithm

按照task就绪时间的先后来运行，每次运行一个任务就更新队列中相关任务的状态

full simulator algorithm

（2）delta simulation algorithm

对于每个新candidate strategy，以上次strategy生成的task graph为基础，只对执行时间轴发生变化的部分所涉及的task进行重新计算。其余任务规划和full simulation algorithm相同

delta simulation algorithm

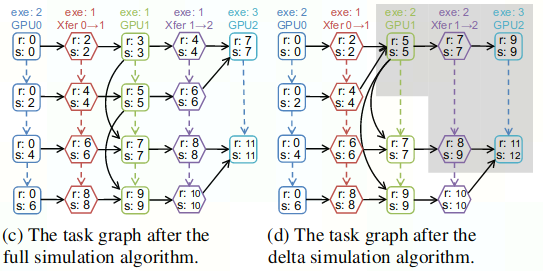
下图中，左侧是full simulation algorithm生成的任务规划图，r为readyTime，s为startTime。右侧为delta simulation algorithm针对新strategy生成的task graph，相比上一个task graph，变化的task只有黑色阴影部分，只需要重新计算这一部分耗时。

任务规划图

Execution Optimizer

输入Operator Graph, Device Topology，输出 Best Found Strategy

寻找最优的并行策略是NP-hard问题，所以采用最小化cost来heuristically explore space

1.MCMC Sampling

将cost转化为概率分布表示，其中 $\beta$ 为常数，

\[p(S) \propto \text{exp} (- \beta \cdot cost(S))\]

由当前策略$S$探索到新的策略 $S^{*}$ 的acceptance criteria，这意味着$cost(S^{*})$比$cost(S)$更小时，$S^{*}$总会被接受，反之也有概率被接受。直观上，MCMC类似gready search，但是可以避免局部最小值。

\[\alpha (S \rightarrow S^*) = \text{min}(1, \text{exp}(\beta \cdot (cost(S) - cost(S^*)))\]

2.Search Algorithm

每次随机选择当前并行策略中的一个op，并将该op的切分配置随机替换

迭代地提出新的candidate strategy ，停止条件：

( 1 )预设的搜索时间耗尽

( 2 )无法在一半的搜索时间内搜索到更优的策略

Ads & DisAds

较为早期的自动并行工作，考虑的问题完备性在当下看起来较为欠缺

优点

  • 提出了新颖的SOPA（Sample-Operation-Attribute-Parameter）四个可切分维度定义的Search Space
  • 构建task graph来确定执行顺序，评估candidate strategy时采用simulator而不是e2e，且采用增量更新

缺点

  • 并未考虑pipeline parallelism，将会导致大量的空泡现象
  • 每个op都单独确定划分行为，复杂度过高；且划分后的每个部分作为一个task单独运行，不能充分利用硬件内存
  • 算法建立在大量建设之上，真实应用将存在问题。例如对通信开销的衡量较为简易，当一个op的input_tensor并不满足该op的切分config时，还需要引入额外的resharding开销

Auto-MAP

paper：https://arxiv.org/abs/2007.04069

概述

并行策略本质是一种计算开销和通信开销之间的trade-off，需要大量专家来定制。

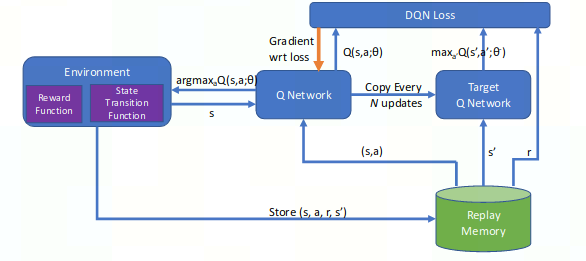
Auto-MAP在HLO IR层面应用RL的方法，来自动生成并行策略（包含DP、OPP、PP）。利用DQN (Deep Q-Network) 算法，结合task-specifical减枝，来search space。大约耗时2h，针对NLP和CV任务都有作用。

Auto-MAP

HLO IR可以看作为一个图

  • node：包含SourceNode（没有input的node）和ComputeNode（HLO指令，可以认为是primitive operator，彼此之间正交）
  • edge：HLO指令之间地dataflow

输入HLO Graph，需要解决三个问题：

  • 数据并行DP：切分SourceNode的维度，使SourceNode到其后继Node之间的通信开销最小
  • 算子划分并行OPP：切分ComputeNode的可训练变量维度，使平均设备利用率最大
  • 流水并行PP：给定期望拆分的stage_num（人为设定的超参数），使cross-stage communication overlap最小

Rainbow DQN（Deep Q-Network)方法

DQN将神经网络作为Q function approximator，本文使用ranbow agent来自动search space。

本文为对DQN算法的修改

  • 扩展prioritized experience replay
  • 丢弃noise linear layers
  • 针对任务调整DNN层数

DQN

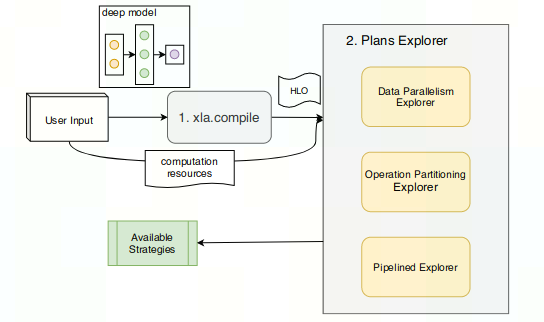
workload

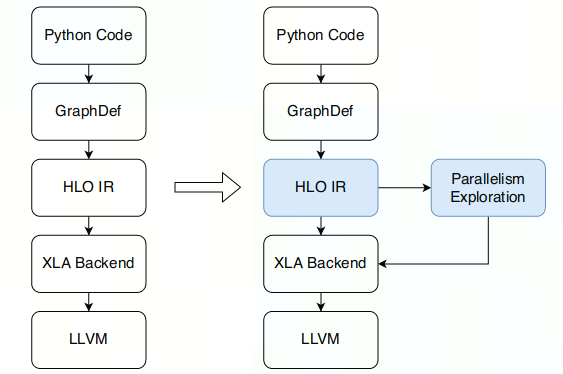
用户输入的model经过xla编译为HLO IR表示，再依次通过Explorer获得并行策略

workload

1.Operator Partitioning Parallelism

只划分model中可训练的变量，使用启发式的方法尽可能地对参数进行划分。

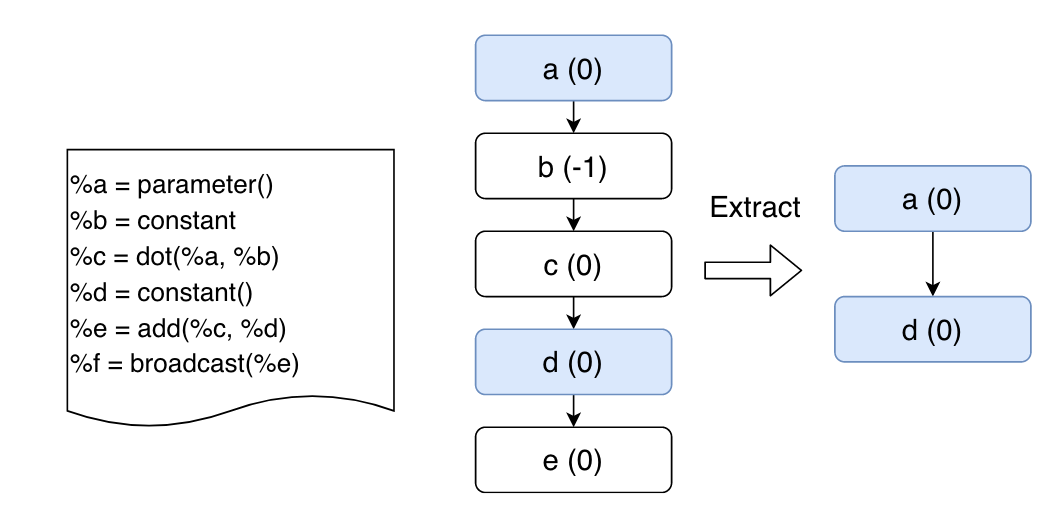
op划分相当于 划分HLO Instruction参数。

每条instruction都设置了推导规则，用于从已知变量/参数的partition中推断出未知变量/参数的partition。

propagation过程：

  • 当给定某些变量/参数的partition时，将对每条instruction施加推导规则
  • 停止条件
    • 没有足够信息进行推导
    • 违反推导规则
    • 所有变量都被推导

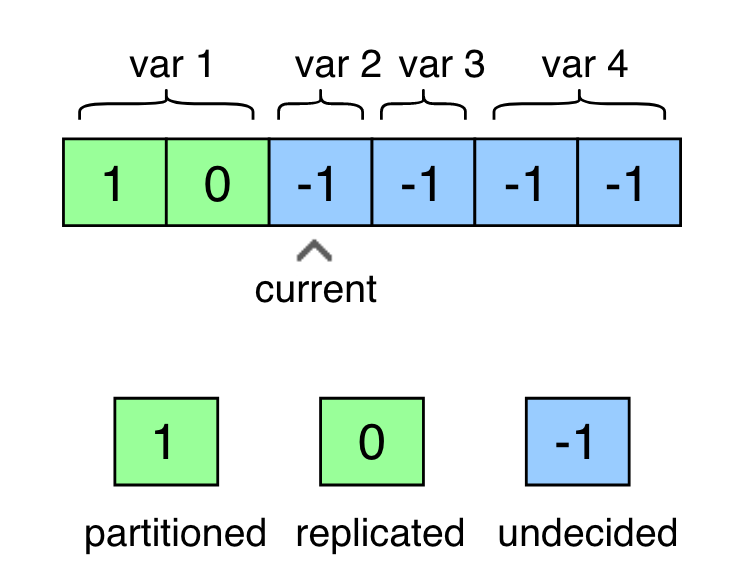
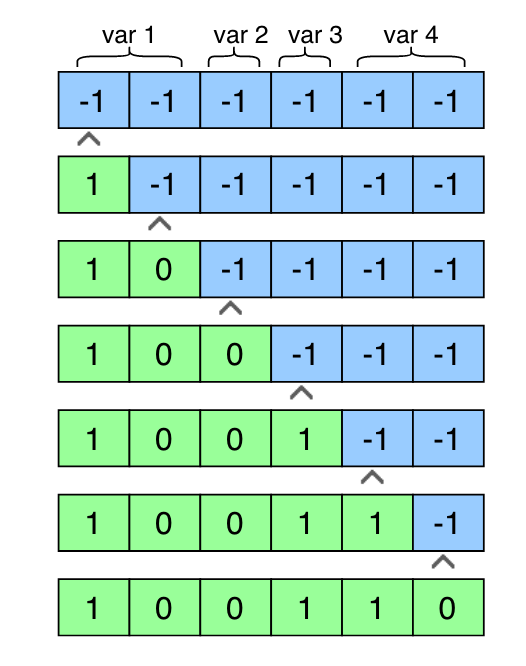
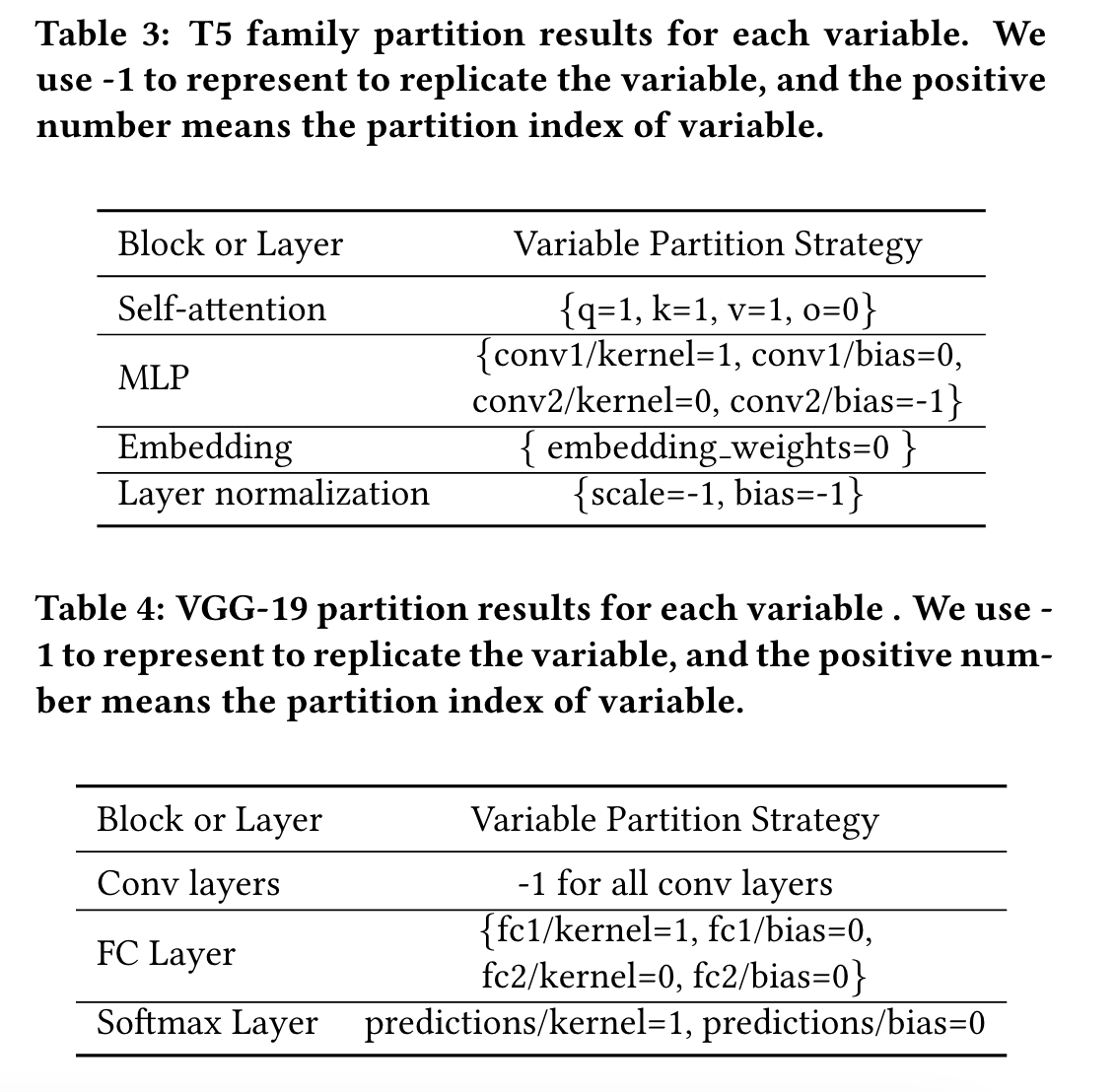
再Auto-MAP中，对每个 可训练变量 的每个 维度（例如NCHW）都要确定partition/replicate

  • state：每个op都有一维向量，包含该op的全体维度划分情况，有三种值，-1、0、1 按原文意思，变量每个维度的策略相同，沿着所有设备划分或者复制

state

  • action：true代表沿着所有设备partition，false代表沿着所有设备replicate
  • reward：partition比replicate有更高的奖励，但是违反设置的推导规则的partition行为将被惩罚

Linkage Group: 记录了由其自身引起的其他可训练变量的确定性划分决策。当选择策略时，能更快确定该策略是否可行，用于启发式减枝。

Linkage Group

2.Auto Data Parallelism

input batch size难以表示→但batch size dimensions遵循dataflow（前向传播）→产生最大数量要划分的张量(尽可能地划分)

action和reward同OPP，但是state是input size的所有划分维度状态

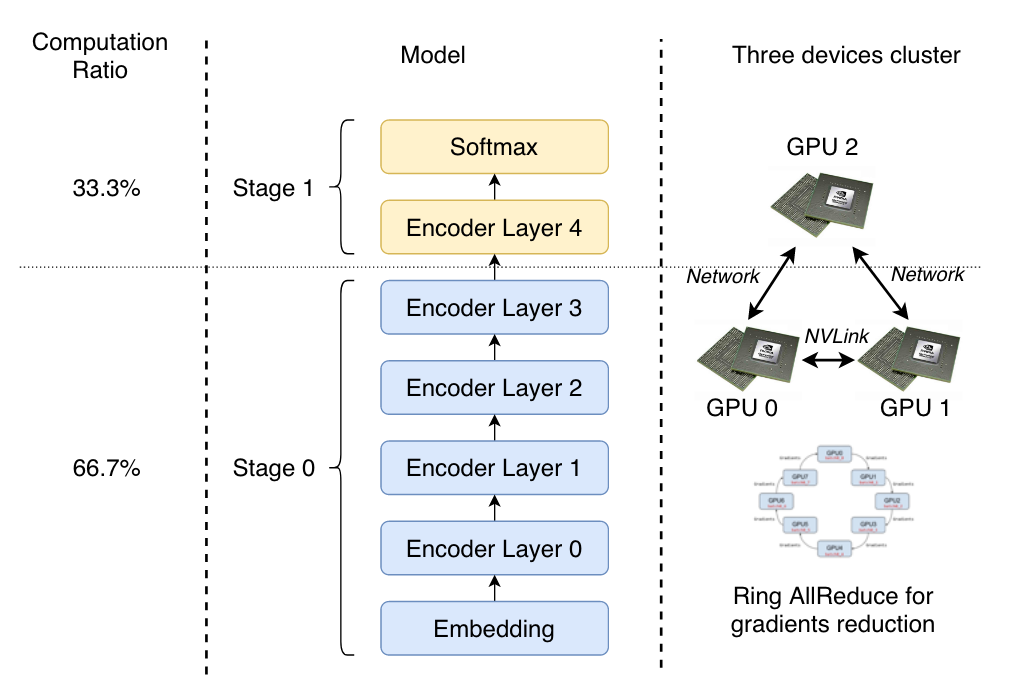
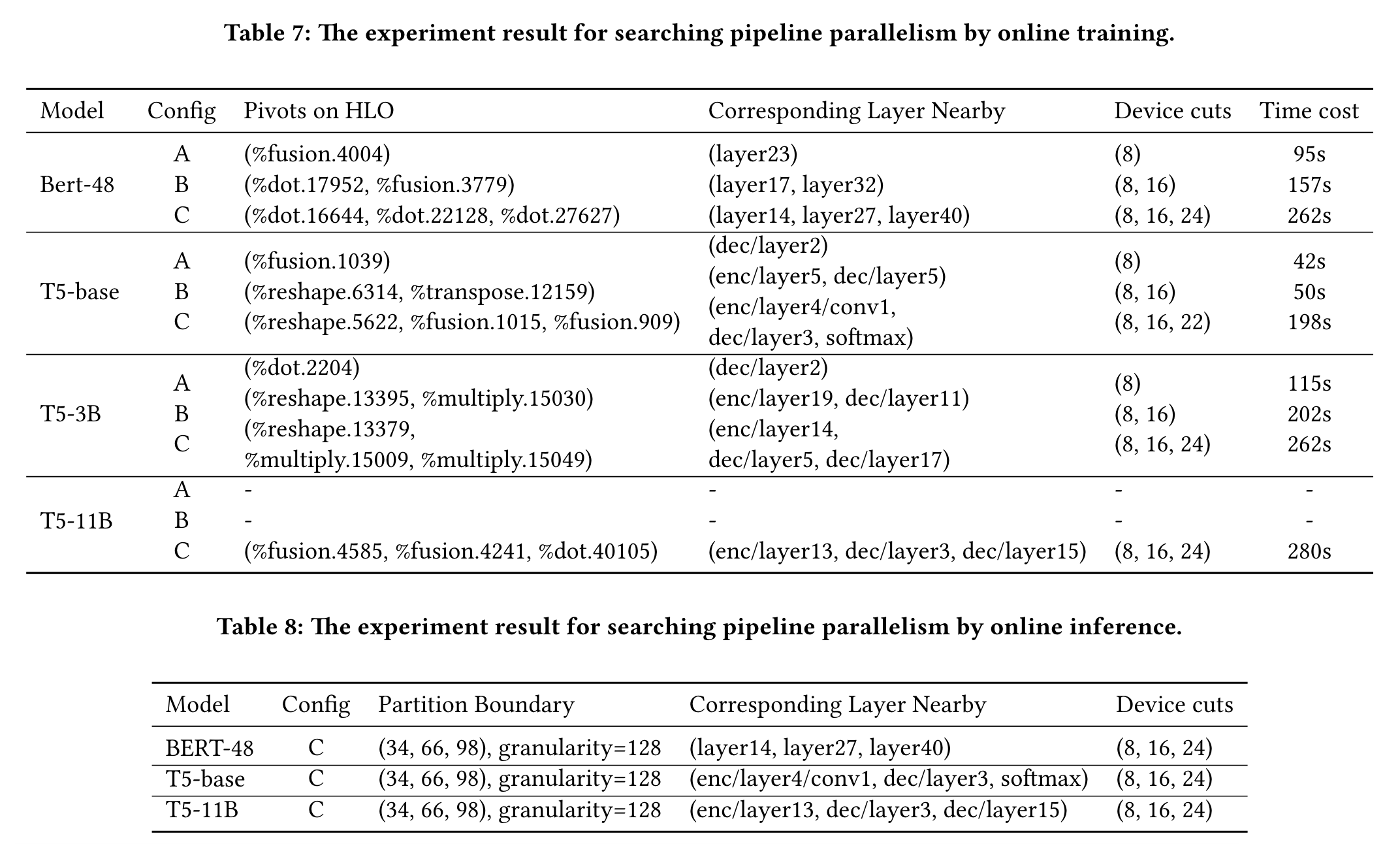
3.Pipeline Parallelism Exploration by Online Training

两个关键点：

  • 将model划分到多个stage
  • 将划分后到情况放在设备上运行
    • 按照每个stage的计算比例来分配计算资源
    • GPU集群中，GPU之间的层级（以链接方式来划分，NVlink/PCI-e等）不同，通信速度也就不同，这适用于不同的任务

划分

Auto-MAP模型

  • state：pipeline的长度L
  • action：如果当前有n个stage，则只会将第n个stage进行切为两份，前n-1个stage不动
  • reward：$\frac{1}{\sqrt{L}}$

4.Pipeline Parallelism by Online Inference

更快速度的方法，有三个重点：

1) partition the model into different stages

2) decide the replication factor for each stage

3) map the stages to underlying hardware devices

给定 HLO 模型 C（per-instruction performance data）、A （activation communication）和 W （parameter sizes），每个数组的长度为原始模型 H 中的指令数，以及最小化端到端的分区 P时间 L，我们可以用我们的值函数来计算：L = V (PC, A,W )

Implementation

采用Rainbow-DCN作为基于PyTorch的DCN框架，利用cost-model(本文中并未说明如何设计的cost-model)来并行地探索上文的三种并行策略。细节请自行看原文

1.Operator Partitioning Parallelism

对于每个op，其每个维度依次决定并行情况

Operator Partitioning Parallelism

linkage group: 选择一个变量及其划分决策，并将这一对发送到propagation模块以推导其他变量的决策。

2.Auto Data Parallelism

尽可能多地划分input batch size

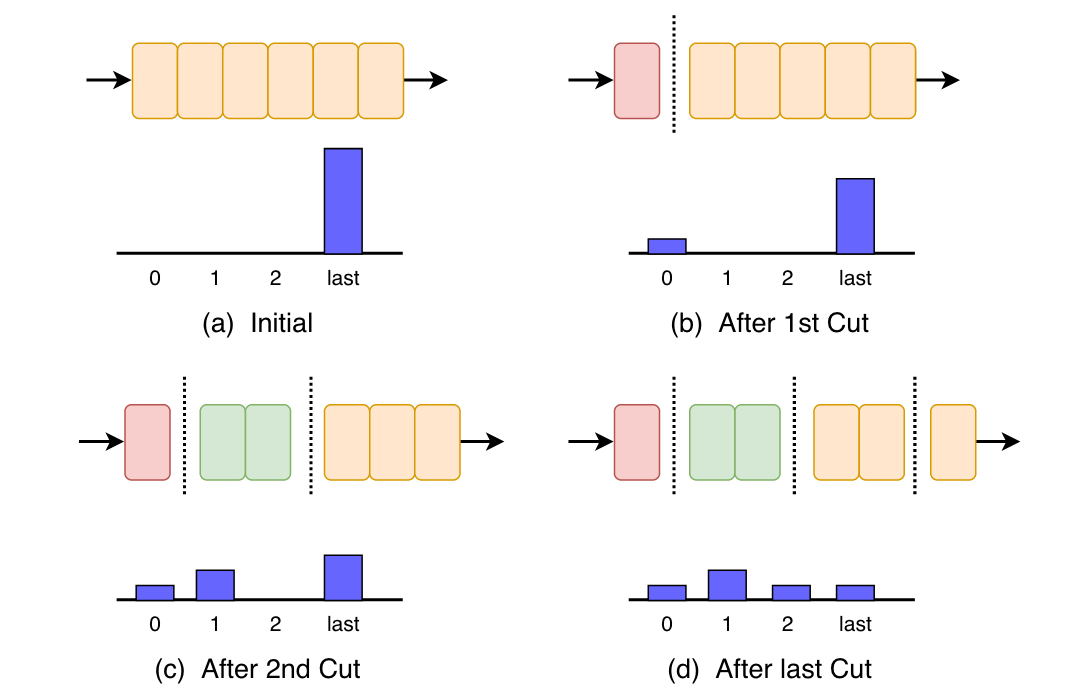
3.Pipeline Parallelism Exploration by Online Training

以网络边界为中心解决方案进行切割的设备切割，期望每个状态的时间成本趋于平衡

1）选择device-cute

2）设定半径

3）得到可行的device-cute方案（还要考虑设备内存的限制）

device-cute

Evaluation

Operator Partition Parallelism

Operator Partition Parallelism

Data Parallelism

Data Parallelism

Pipeline Parallelism

Pipeline Parallelism

GSPMD

reading

Alpa

（我读该领域的第一篇，所以比较详细qwq）

paper： Alpa: Automating Inter- and Intra-Operator Parallelism for Distributed Deep Learning

repo：https://github.com/alpa-projects/alpa

Alpa: Automating Inter- and Intra-Operator Parallelism for Distributed Deep Learning

在一定时间内（40min左右），自动对DL模型做分布式策略规划，输入为computation graph（静态图、以HLO IR形式表达）、device cluster

概述

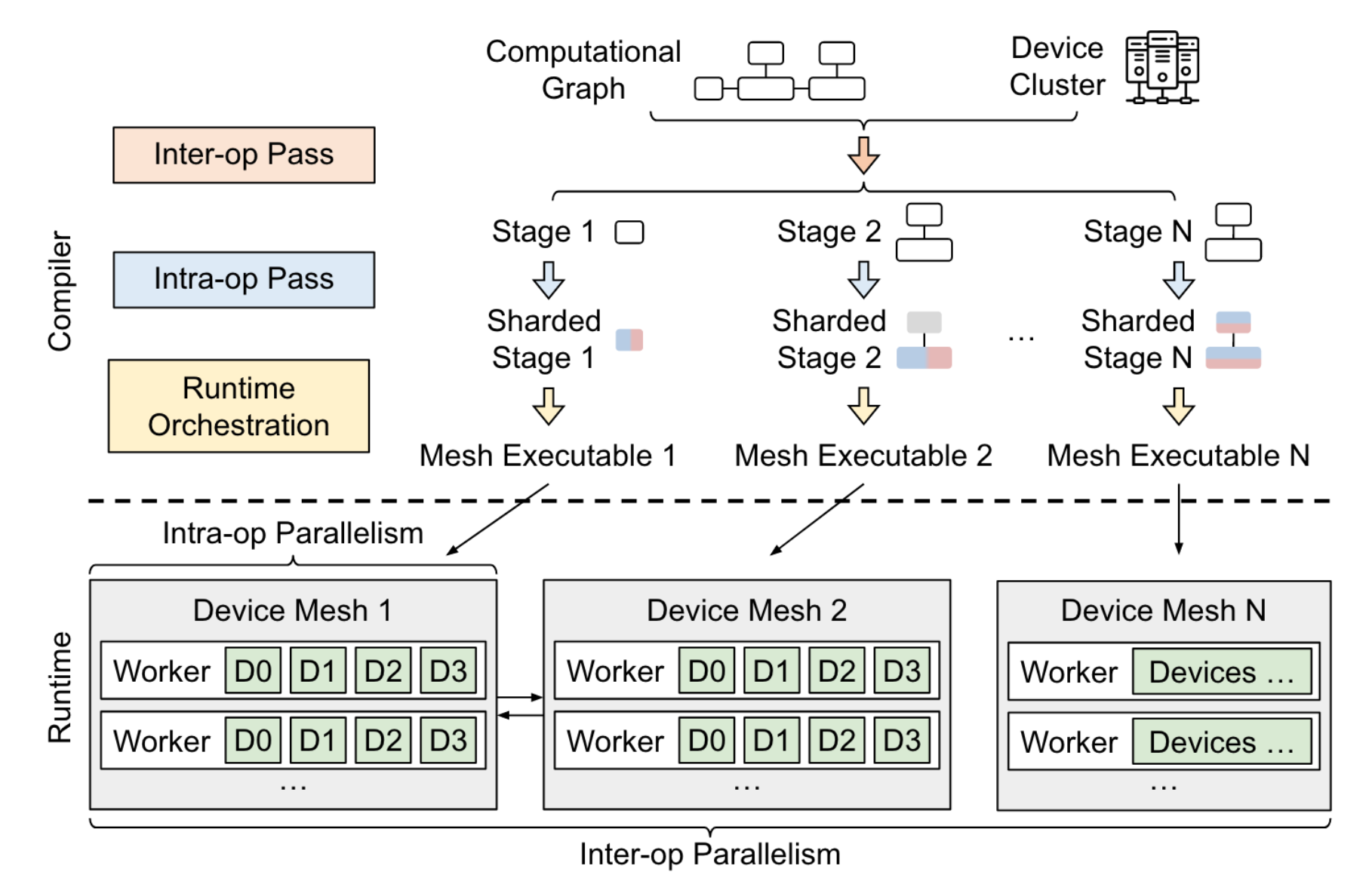
Alpa将并行策略分为

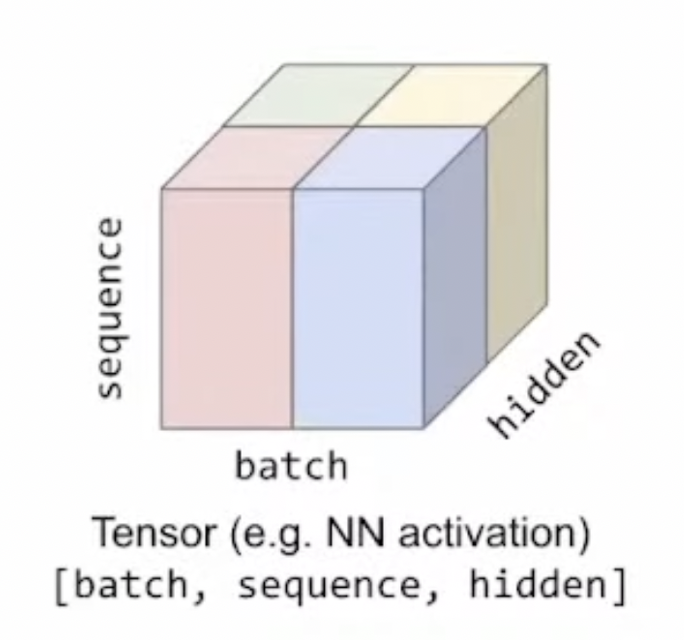
  1. Intra-Operator Parallelism：将tensor按某些维度（一般有batch、channel、height、width）切分，放到不同device上计算

Intra-Operator Parallelism

  1. Inter-Operator Parallelism：将计算图切分为多个计算stage，放在不同的device-mesh上计算

Inter-Operator Parallelism

为什么分为这两种并行：

（1）这两种并行可以表示常见的并行种类：intra-op parallelism如果对batch维度切分就是数据并行，对非batch维度切分就是常见的算子内并行（张量并行）；inter-op如果切点合适，计算stage之间只存在一条传递数据依赖，则可以变种为pipeline parallelism（第一个stage每次只执行1/B个batch）

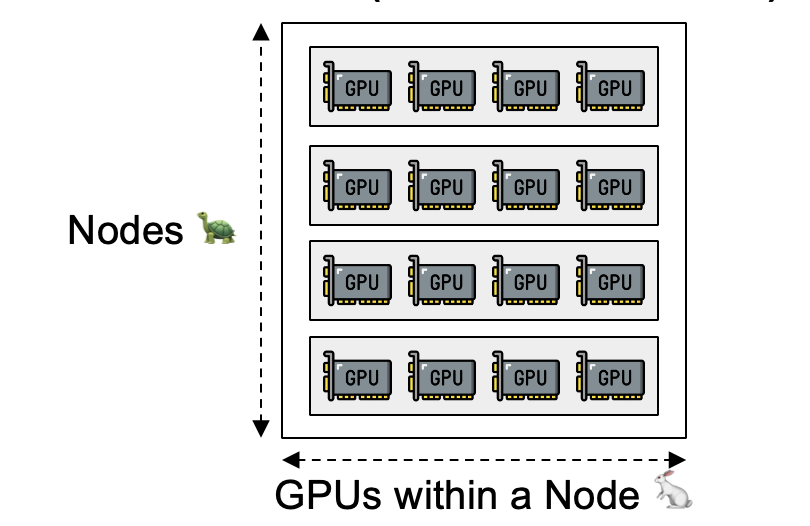
（2）这两种并行和device cluster的层次结构匹配：

将Intra-op Parallelism映射到高带宽互联的devices上（距离较近的设备）

将Inter-op Parallelism映射到低带宽互联的devices上（距离较远的设备）

层次结构匹配

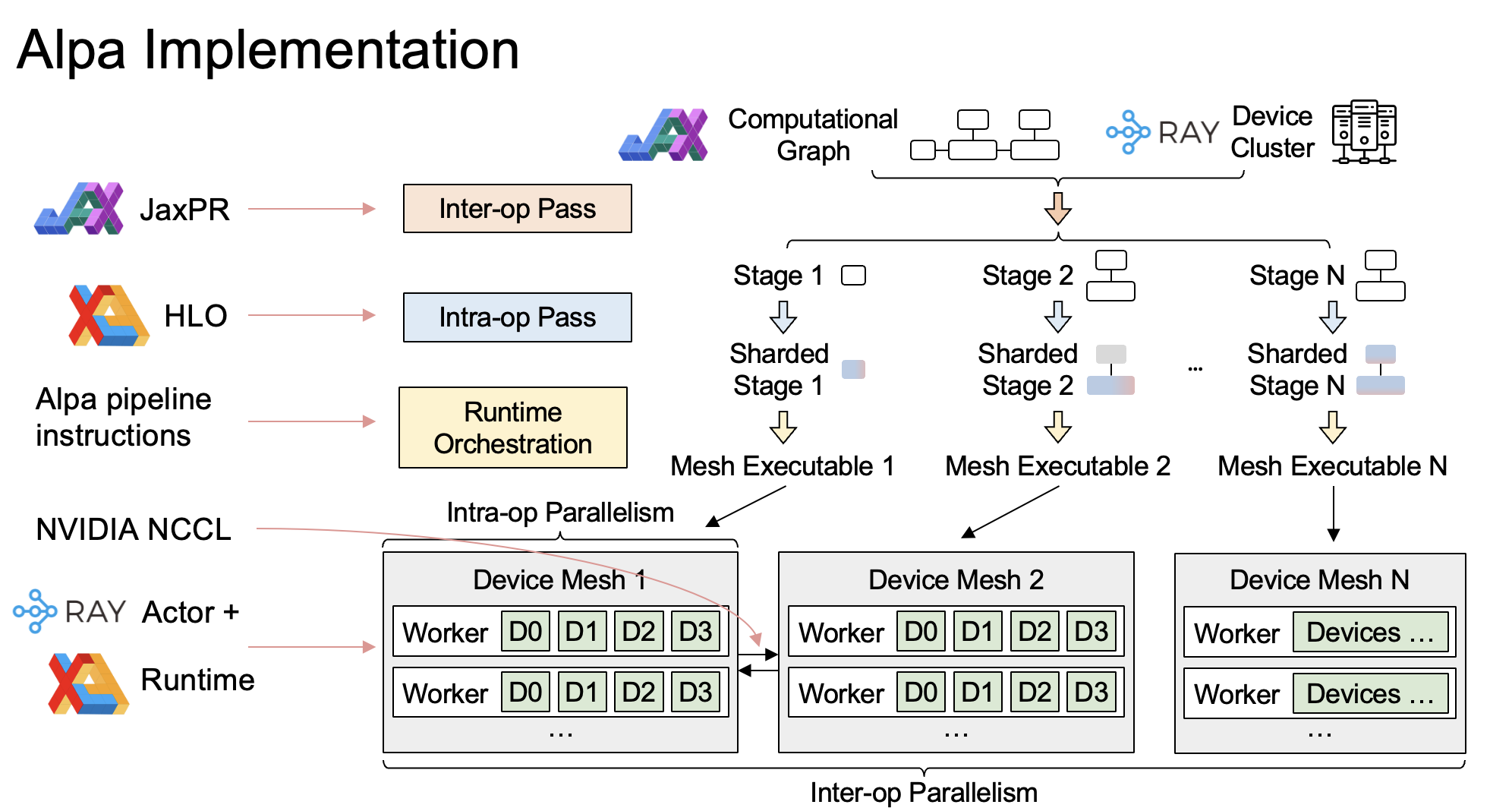
Alpa的runtime会协调这两级并行，在两级空间中分别探索最优解：

子结构（stage-mesh）最优（执行开销最小）+ 子结构之间的通信开销最小—>并不能保证全局最优

stage-mesh

Runtime Orchestration pass：系统优化、cross-mesh通信等

Intra-op Parallelism

将 stage 内 op 对应（input） tensor 沿某些维度划切分，分配到 mesh 内的多个device上计算

1.对op进行切分，给切分的op片段分配device

（1）如果找到op切分策略后，再给切分op分配执行的device，双重枚举会导致复杂度爆炸增长

（2）前提：mesh内的设备算力相同—>op 在多设备上均匀划分可以显著缩减 intra-op plan 的搜索空间

—>

将op的sharding spec（描述了tensor切分行为）和device mesh映射对应—>op的sharding spec表示切分，同时表示切片部分由哪些device执行（在对应device上的行为）

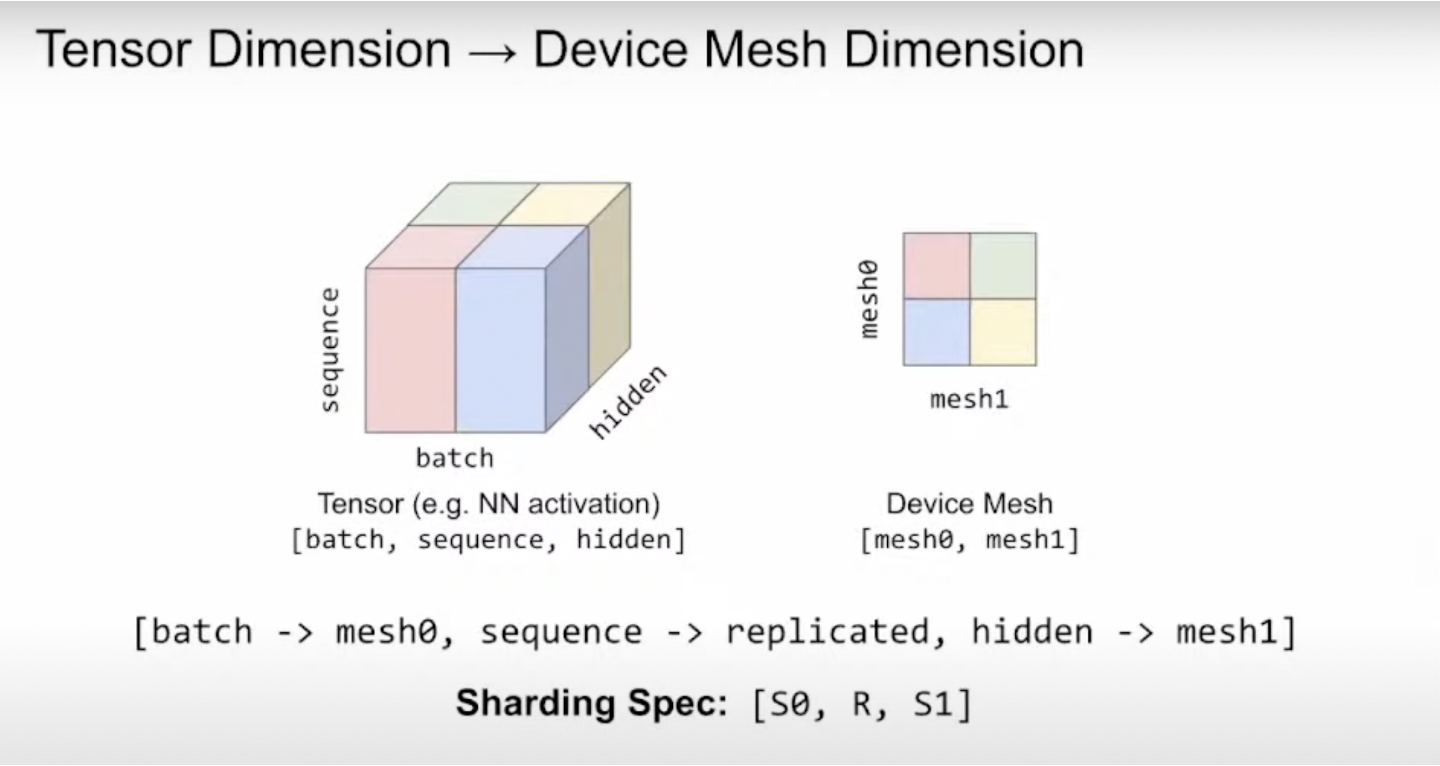
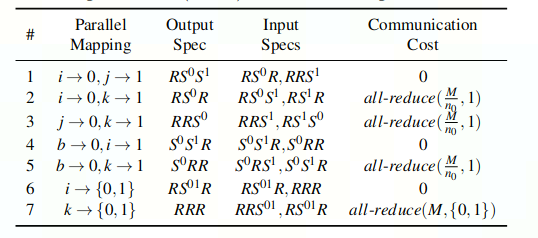
对于一个N维（非batch轴个数）的tensor ，定义其切分方案sharding spec为$[X_0, X_1, \dots , X_{N-1}], (X_i \in {S, R})$ ，S和R分别表示（沿着非batch维度）sharding和replicate。$X_i = S^j$ 表示 使用沿着mesh的第j维的设备 对 tensor的第i维进行切分

以2D（NxM） Tensor到2D（axb） Mesh Device的所有切分与映射说明

映射说明

每个op的sharding spec为$X_0 X_1$，$X_0$表示沿tensor的第0维（沿列=按行）切分情况，$X_1$表示沿tensor的第1维（沿行=按列）切分情况

S和R分别表示（沿着非batch维度）sharding和replicate，$S^0$表示该维度沿着mesh的第0维（沿列）做切分，每一列的设备执行op中完全不相交的部分，每一行设备执行完全一致的任务；$S^1$表示该维度沿着mesh的第1维（沿行）做切分，每一行的设备执行op中完全不相交的部分（数据并行，batch切分），每一列设备执行完全一致的任务（数据并行，batch切分）

$S^0$和$S^1$有且只能出现一次

sharding spec图解：

sharding spec

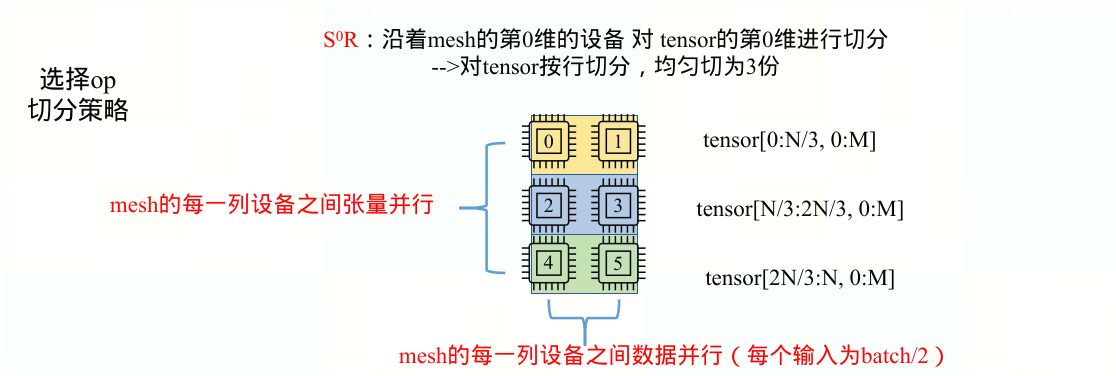
$S^0R$：tensor沿列（按行）切分为a份，每份[N/a, M]，mesh中第i（0≤i<a）行中所有device都执行op的[N/a * i, M] —> 沿mesh第0维（沿列）张量并行（张量被横向切分）+ 沿mesh第1维（沿行）数据并行（每个输入为batch/b）

S0R

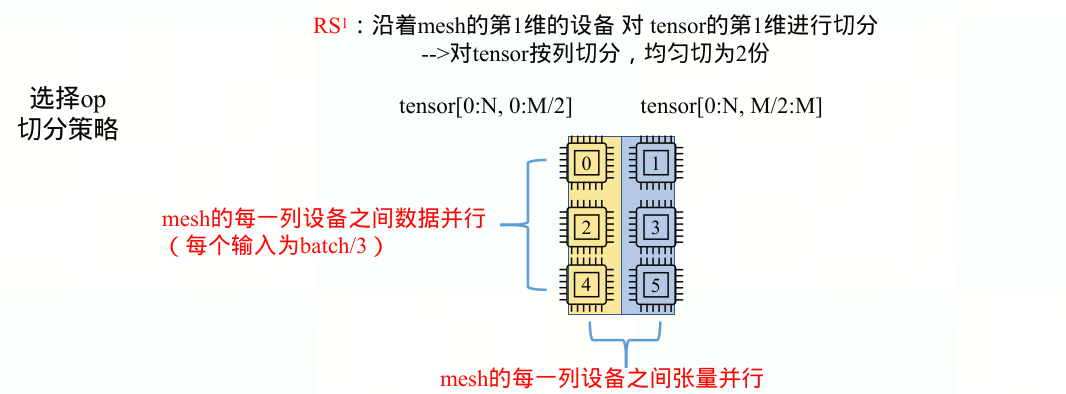
$RS^1$：tensor沿行（按列）切分为b份，每份[N, M/b]，mesh中第j（0≤j<b）列中所有device都执行op的[N, M/b * j] —> 沿mesh第1维（沿行）张量并行（张量被纵向切分）+ 沿mesh第0维（沿列）数据并行（每个输入为batch/a）

RS1

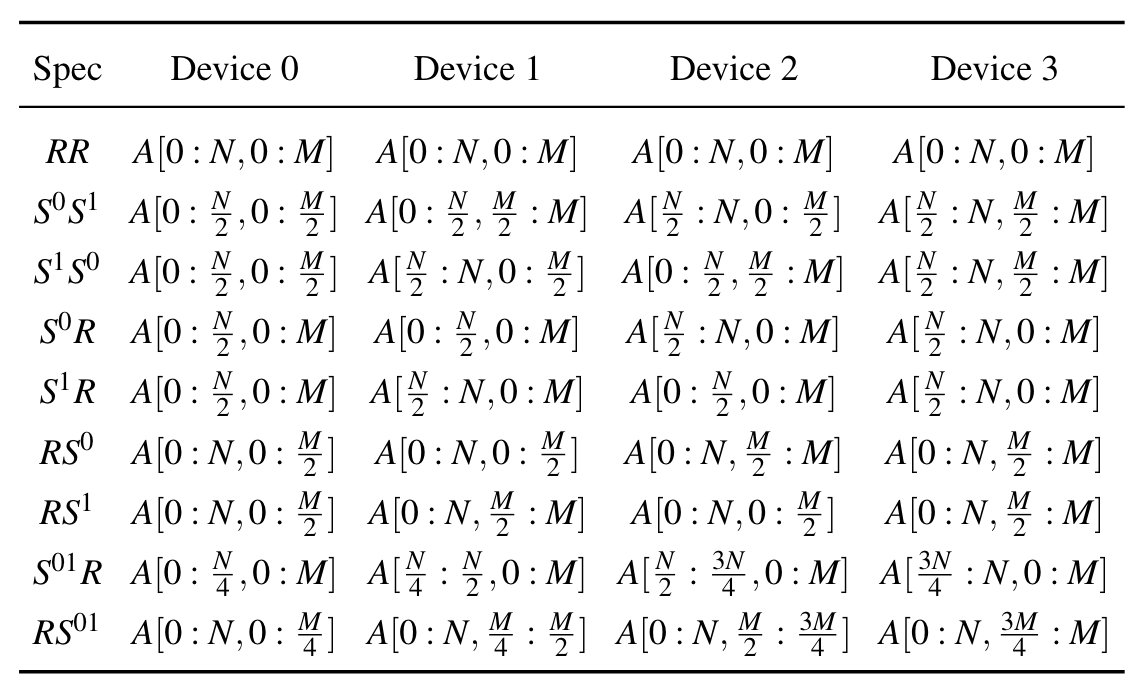
下图列出了Tensor（NxM ）到Mesh Device（2x2）的所有切分与映射示例。数字代表device标号，颜色表示op的tensor分片

切分与映射示例1

切分与映射示例2

（3）对于每个op，由其input tensor shape可以推导出output tensor shape，反之亦然。故由output切分可以推出input切分，这种推导规则被称为parallel algorithm。

每种operator可能会有多条推导规则（对应多种output切分），有些algorithm会引入一些通信补偿保持数学等价性，下表是batch matmul（$C_{b,i,j} = \sum_{k}A_{b,i,k}B_{b,k,j}$）的多条parallel algorithm的示例（shrading spec有3位，是在显式地拆分batch）

推导规则

由于model是以XLA的HLO IR格式表示，其中常见的DL运算符可以总结为不到80个primitive operators，因此对于每个op都列举出parallel algorithm表格。这样就可以为每个operator选择一个parallel algorithm，目标整体stage-mesh的execution cost最小

2.stage执行开销=sum(op执行开销+其他开销)

\[\min_{S} \sum_{v \in V} s^T_v (c_v + d_v) + \sum_{(v,u) \in E} s^T_v R_{vu} s_u\]

其中$k_v$为op v的所有parallel algorithm可能，$s_v \in {0, 1}^{k_v}$为op v选择paralle algorithm的情况

（1）op v执行开销 = $s_v^T(c_v + d_v )$ = 计算开销+通信开销

  • 计算开销：所有的op的computation cost均为0
    • 对于计算开销大的算子（matmul），一定会将tensor拆分给每个设备，所以每个设备的计算开销均等
    • 对于计算开销小的算子（element-wise），可以忽略
  • 通信开销 = 当前parallel algorithm所需要的通信补偿（查op的parallel algorithm表格）

（2）其他开销 = $s_v^T R_{vu} s_u$

$s_v, s_u$分别为op v和op u选择paralle algorithm的情况，$R_{uv}$是一个矩阵，$R_{uvij}$是从op v的第i个策略的输出到op u的第j个策略的输入的resharding成本。

假设op u的输入来自于op v的输出，但op u的输入tensor切分情况与op v的输出tensor不符合，就需要resharding开销

resharding

（3）求解：使用ILP求解“stage执行开销最小”问题

  • 由于其他开销 $s^T_v R_{vu} s_u$是二次的，所以引入变量$e_{uv} = {0, 1}^{k_v, k_u}$来线性化这一项
  • 简化graph（算子融合）：将计算简单的op（element-wise、transpose、reduce）与其操作数对应的op融合，并从操作数开始传播更新sharding spec

3.post intra-op pass：通信优化，使用reduce-scatter和all-gather替换all-reduce，这就实现了ZeRO中权重分片的效果

Inter-op Parallelism

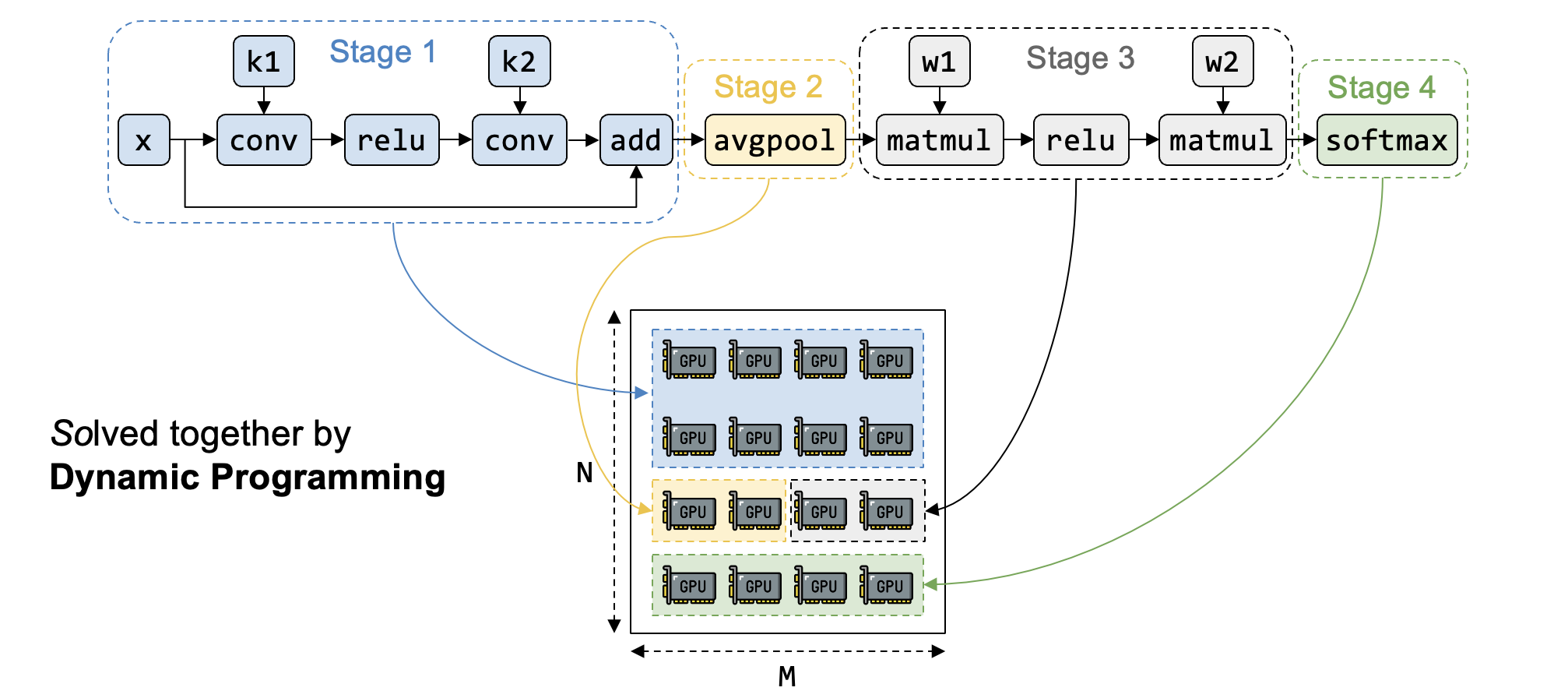
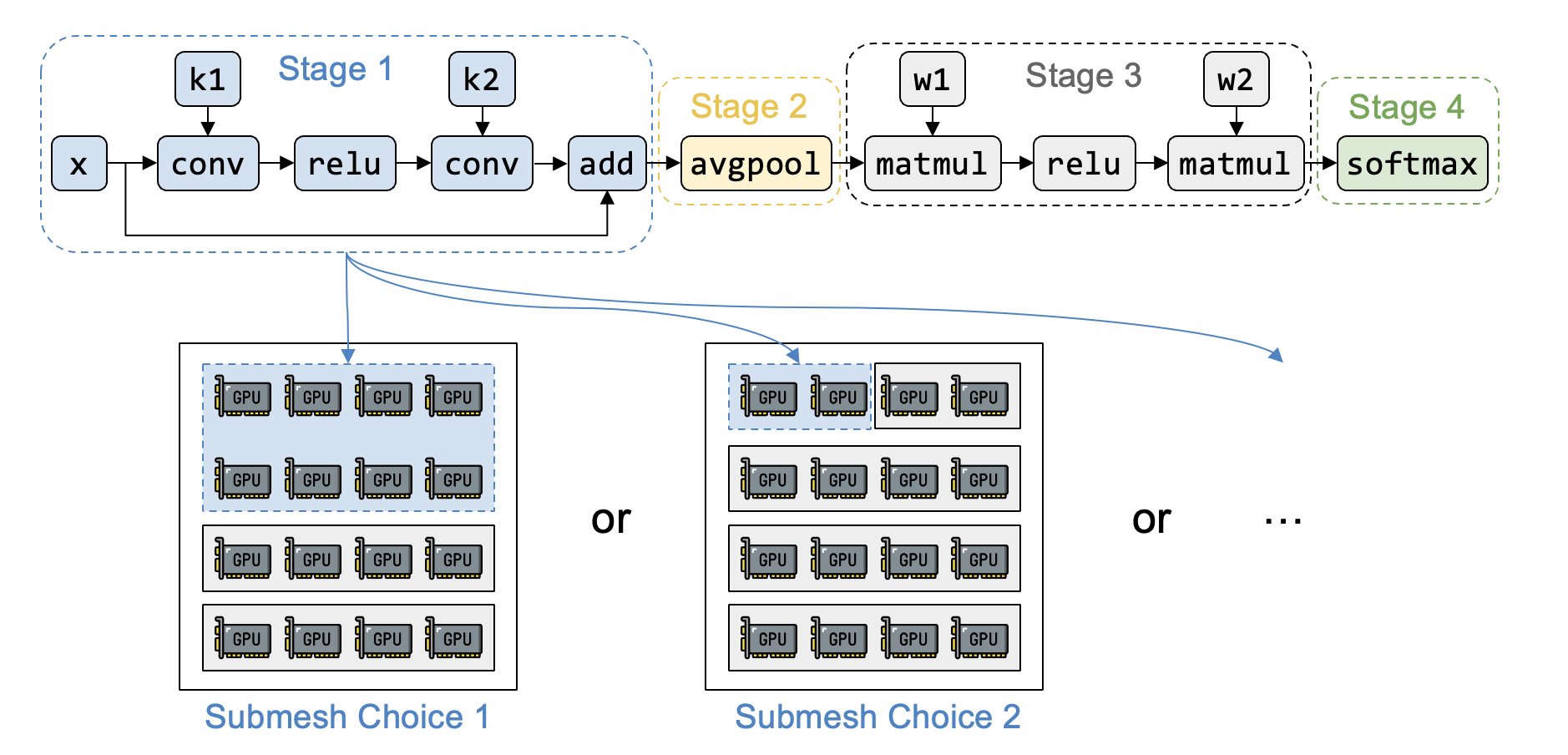
将计算图的op（按拓扑序）组织为stages，将device cluster划分为device meshes，每个stage在对应的device mesh上执行—>stage-mesh pair

Inter-op Parallelism

计算图按照user define的顺序进行拓扑排序，得到算子列表记为$(o_1, \dots , o_K)$，算子$o_k$的输入来自于$(o_1, \dots , o_{k-1})$。一共分为S个stage，为$(s_1, \dots, s_S)$，stage $s_i$包含的op有$(o_{li}, \dots, o_{ri})$，并且分配device mesh $(n_i \times m_i)$

mesh可选 shape 的限制：为了不浪费cluster mesh (N*M，N台机器，每台机器M个节点/device)的计算资源，并保证device之间更高的通信带宽，mesh一般整选取 (2, M)、(3, M) …… (N, M)

mesh可选 shape 的限制

1.计算图总开销最小

记$t_i = t_{intra}(s_i, Mesh(n_i, m_i))$为stage $s_i$的stage execution开销，由intra-pass中ILP solver获得，故计算图总开销为$T = \min\limits_{{(s_0, Mesh(n_0, m_0)),\dots,(s_S, Mesh(n_S, m_S)}} \sum_{i=1}^{S}t_i$

由于计算stage之间只存在一条传递数据依赖，令第一个stage每次只执行全部输入的1/B个batch—>引入pipeline parallelism

pipeline parallelism

因此，计算图的总开销（即pipeline执行开销）为：B为超参数，microbatch=batch/B

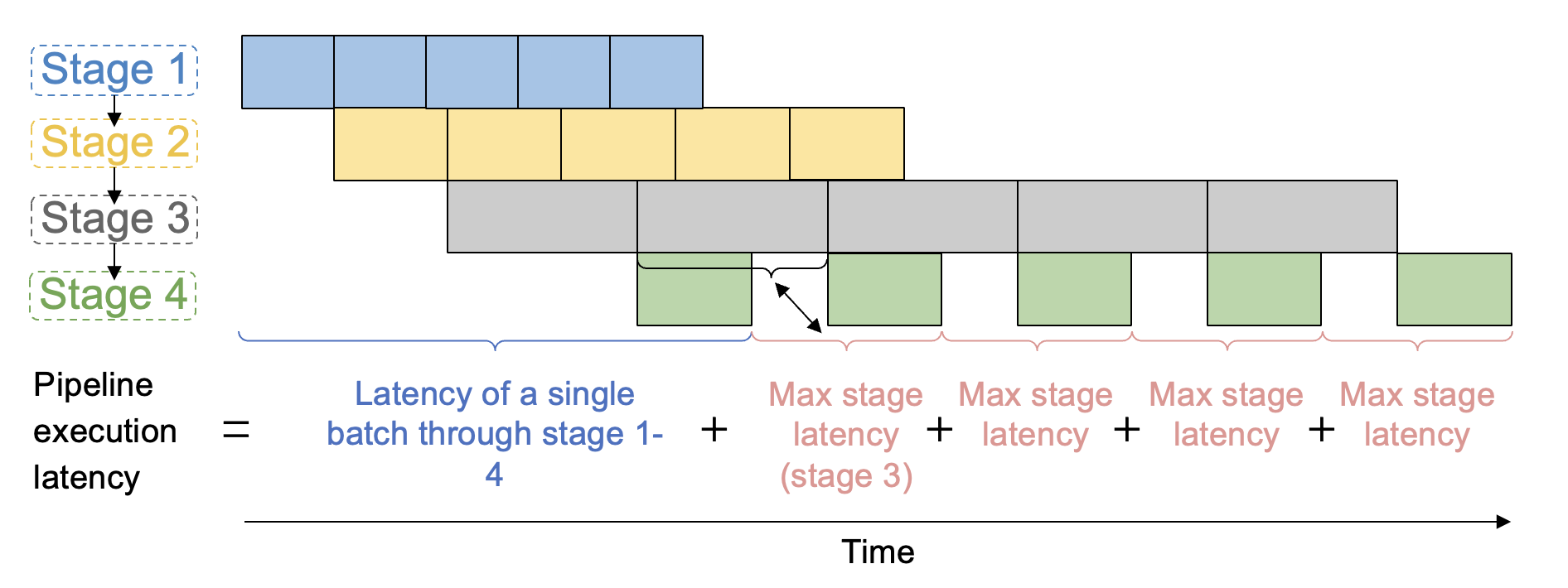
$T^* = \min\limits_{{(s_0, Mesh(n_0, m_0)),\dots,(s_S, Mesh(n_S, m_S)}} {\sum_{i=1}^{S}t_i+(B-1)\max\limits_{1\le j \le S}{t_j}}$

其中

  • $\sum_{i=1}^{S}t_i$ 为第一个microbatch经过所有stage的耗时（latency）；
  • $(B-1)\max\limits_{1\le j \le S}{t_j}$为剩下（B-1）microbatch的耗时，受最慢stage大影响

如果只保留该公式的第二项，即要求最大stage耗时最小，是不合理的。引用一篇博客的解释

“

（1）极端情况下可能是每个op一个stage，这样的Pipeline吞吐必然是低效的

（2）这个公式的第一项和第二项可以分别解释为warmup phase和stable phase，同时优化这两个目标在同步版本的pipeline上非常重要，因为每一个iteration都会包含这两个phase。

”

求解方式：枚举第二项全部的可能值，将其一项转化为一个2维背包问题

故问题可以转化为：

固定 $t_{max}=\max_{1\le j \le S}t_j$，最小化$t_{total}(t_{max}) = \sum_{i=1}^{S}t_i$

引入 $F(s,k,d|t_{max})$ 来表示“将算子序列 $(o_k, \dots , o_{K})$ 分配到s stage、使用d个设备运行”的最小耗时

初始条件 $F(0,K,0 | t_{max}) = 0$，F的求解公式如下

F的求解公式

$t_{intra}((o_k, \dots , o_i), Mesh(n_s, m_s),s)$来自于intra-op pass的输出，输入为算子序列$(o_k, \dots , o_i)$$(o_k, \dots , o_i)、 Mesh(n_s, m_s)$，其中mesh还需要枚举所有可能$n_l \times m_l = n_s \times m_s$，以获得最优开销。同时选择的策略需要满足内存需求（执行stage、存储中间结果）

最终inter-op pass的问题转化为 $T^{*} (t_{max}) = \min\limits_{s}F(s,0,N\times M|t_{max}) + (B-1)t_{max}$

2.优化DP问题复杂度

（1）early pruning：从0开始枚举$t_{max}$，当$B \cdot t_{max}$ 大于当前最优$T^*$时，停止枚举

（2）operator clustering：将相邻 op 合并为一个 layer，以减小图规模。合并目标包括两类：1) 计算量较小的 op；2) 若放置在不同设备 mesh，会带来连续通信的相邻op

使用多个worker并行的编译stage

编译stage

3.最优执行总时间公式再思考

$T^* = \min\limits_{{(s_0, Mesh(n_0, m_0)),\dots,(s_S, Mesh(n_S, m_S)}} {\sum_{i=1}^{S}t_i+(B-1)\max\limits_{1\le j \le S}{t_j}}$

其中

  • $\sum_{i=1}^{S}t_i$ 为第一个microbatch经过所有stage的耗时（latency）；
  • $(B-1)\max\limits_{1\le j \le S}{t_j}$为剩下（B-1）microbatch的耗时，受最慢stage大影响

如果只保留该公式的第二项，即要求最大stage耗时最小，是不合理的。引用一篇博客的解释

“

（1）极端情况下可能是每个op一个stage，这样的Pipeline吞吐必然是低效的

（2）这个公式的第一项和第二项可以分别解释为warmup phase和stable phase，同时优化这两个目标在同步版本的pipeline上非常重要，因为每一个iteration都会包含这两个phase。

”

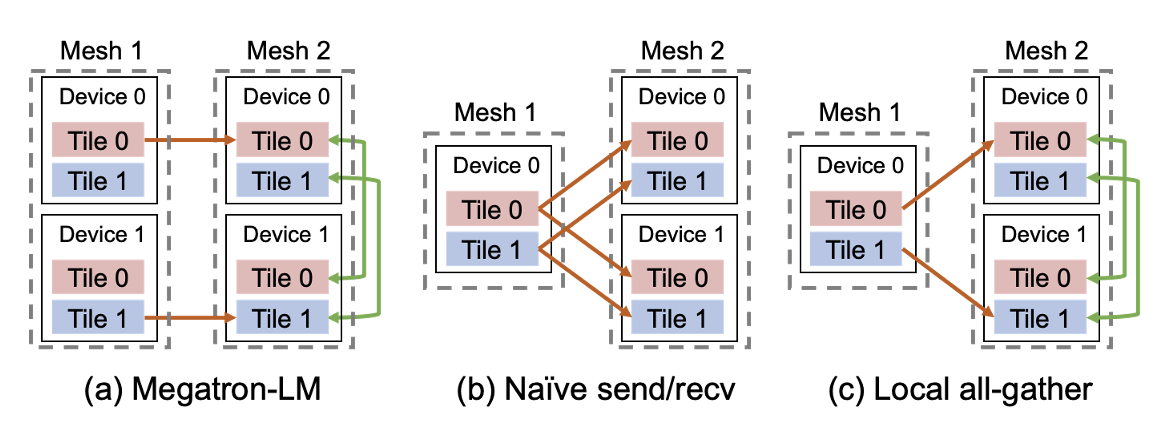
Parallelism Orchestration

  • 必要时插入集体通信原语来解决intra-op pass引起的mesh内部通信
  • cross-mesh resharding：优化通信，从p2p到all-gather

cross-mesh resharding

整体架构

整体架构

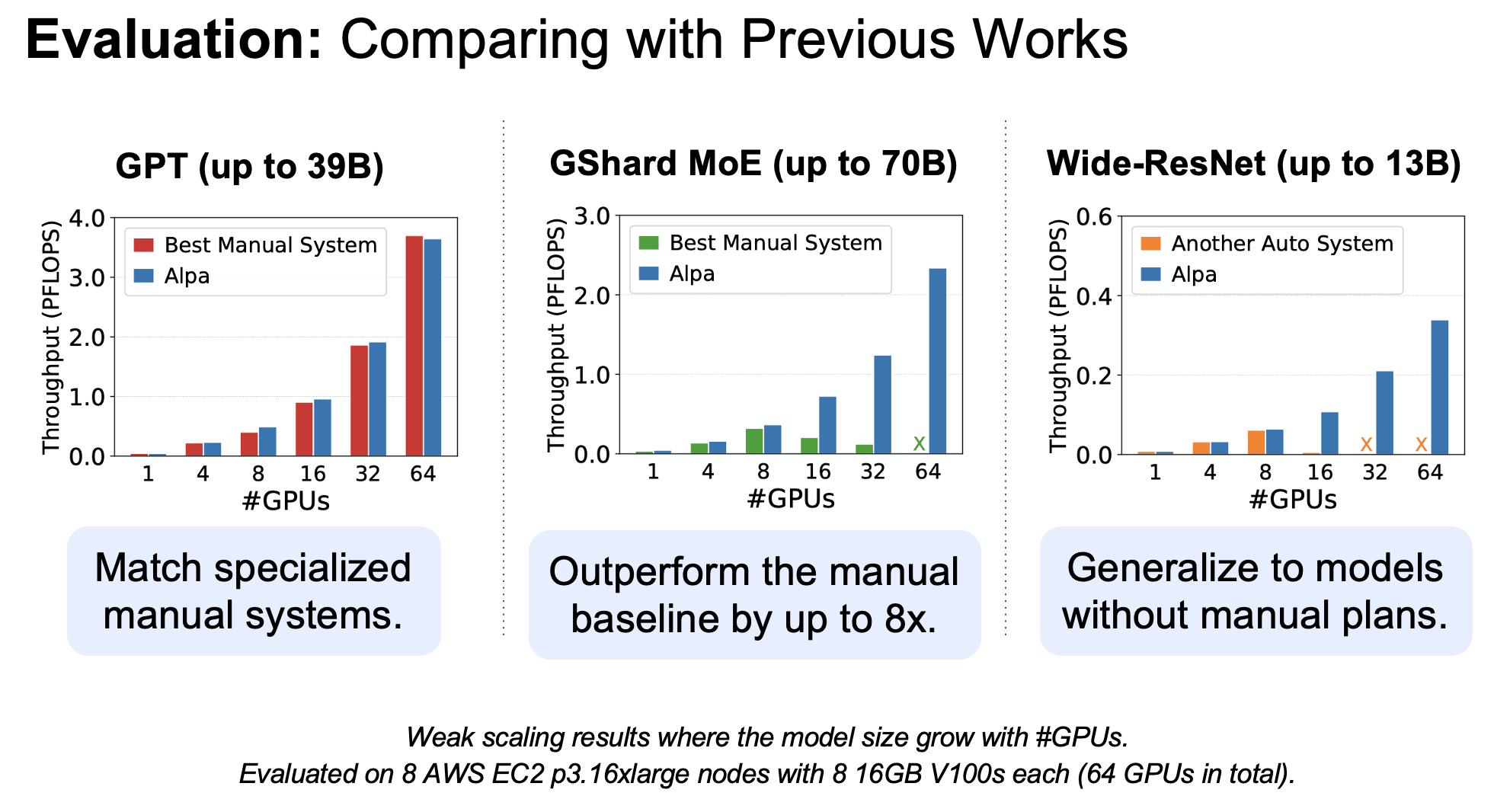
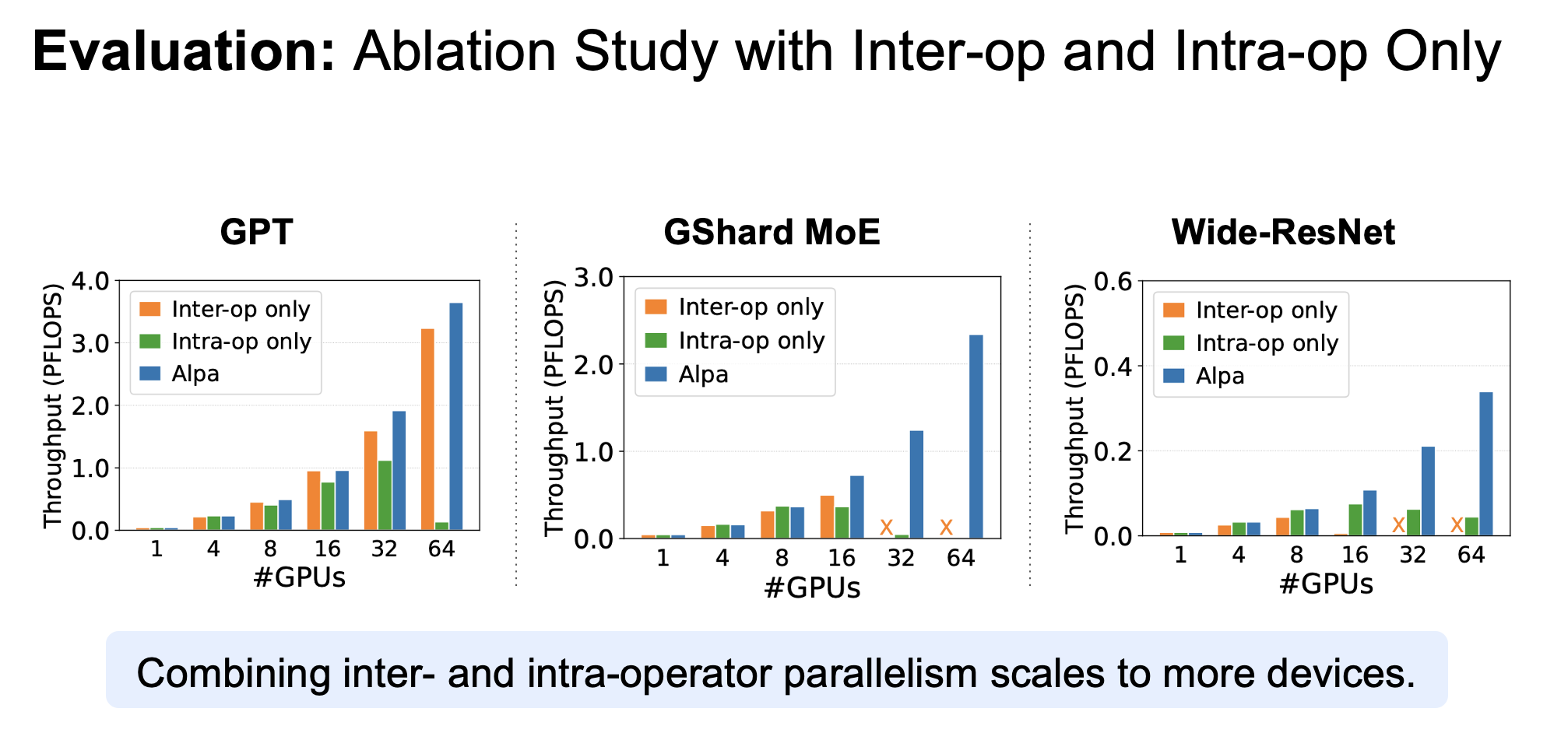
Evalution

媲美极致手工优化的性能，针对没有手工优化的baseline也能有不错的吞吐

Evalution

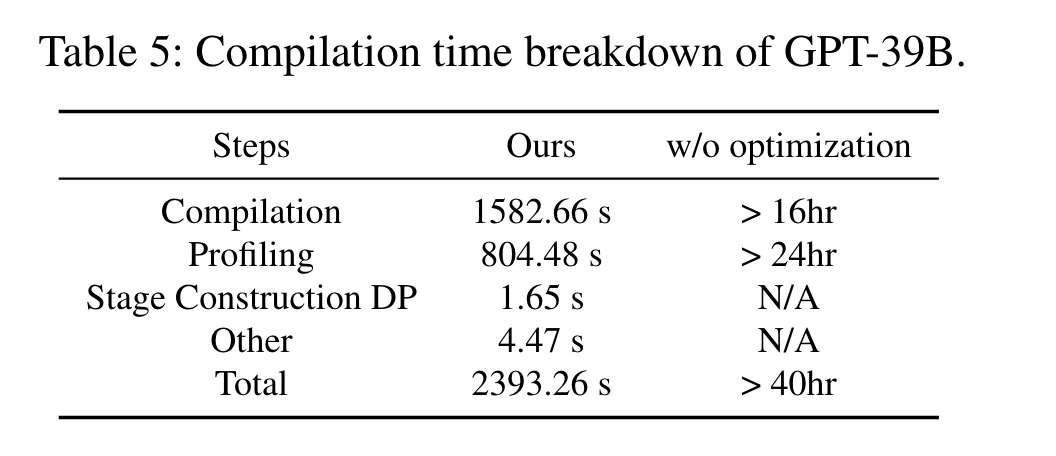
以GPT-39B为例，主要耗时在枚举stage-mesh pairs以及profiling（获取staged latency 和内存需求）

耗时1

ablation

Ads & DisAds

优点

  • 根据device之间的通信带宽能力，将并行分级为inter-op和intra-op
  • 对op（tensor）的切分行为同时确定了运行的设备
  • 对问题的建模使用ILP和DP求解，不同于RL或LLM依赖大量数据集

缺点

  • 只适用于静态图、静态shape
  • inter-pass中需要一个超参数B来规定流水并行中microbatch的大小
  • 计算图总开销公式中并没有建模cross-mesh通信的开销（operator clustering压缩了可能的通行量+通信优化 ⇒ 可以忽略不计？）

TePDist

paper：Auto-Parallelizing Large Models with Rhino: A Systematic Approach on Production AI Platform

repo：https://github.com/alibaba/TePDist

概述

使用HLO IR表示model，使用 client/server mode实现分布式策略和模型描述解耦（方便其他框架接入）

  • server：使用HLO IR作为input，自动探索分布式并行策略
  • client：将model描述转化为HLO IR（任意可以将model转化为HLO IR来表示的client都可以接入）

提供多级别优化探索：

  • 高级别O3：追求分布式策略的质量
  • 低级别O2：采用额外的启发式算法，牺牲策略质量，换取搜索速度

分解策略搜索问题为子问题优化，再分散地解决子问题

pipeline parallelism：将stage划分建模为ILP问题，ILP Solver以总通信开销最小为目标

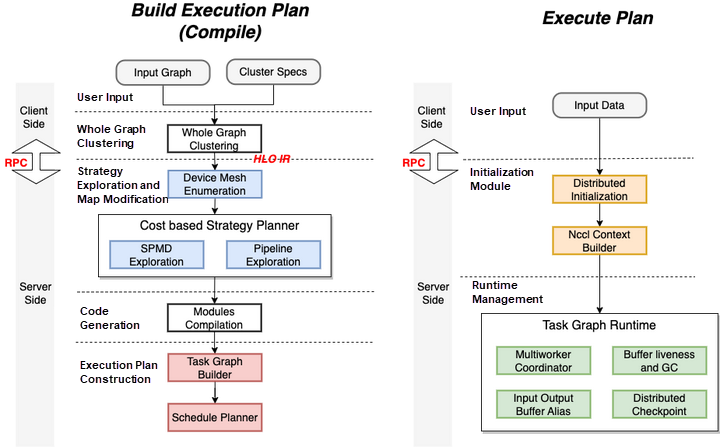
Architecture

  • 编译阶段
    • automatic distributed strategy search
    • device mesh allocation
    • TepDist execution engine construction(task graph construction and static scheduling order determination for the task graph)
  • 执行阶段：the client sends the data input command to execute the plan

Architecture

SPMD Strategy

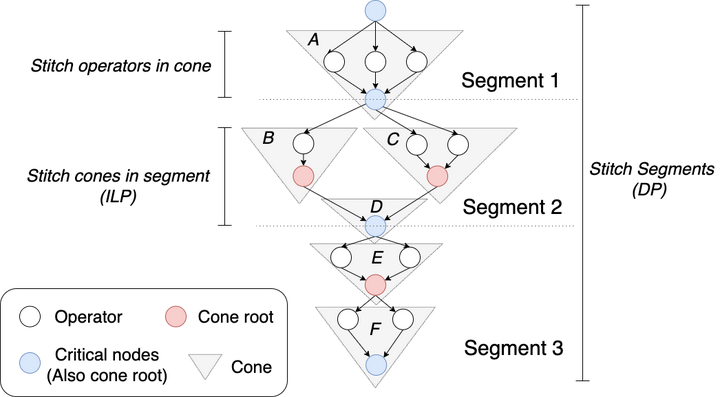
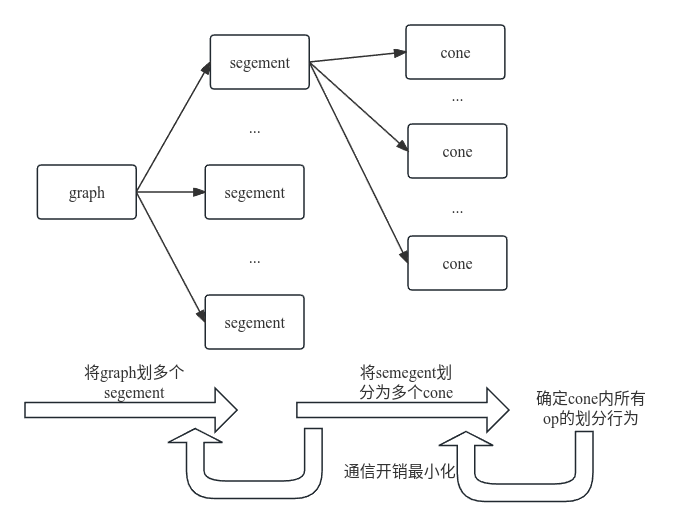
SPMD策略：无需对庞大的DAG线性处理，而是按照三个层级

SPMD策略

cone（op的tensor的切分）→segment（cone的切分）→graph（segment的切分）

  • cone
    • 由root（多个节点/计算量很大）和非root节点组成，DAG中有很多，一般呈现倒三角
    • 用cone来粗粒度地表示节点，需要对每个cone都决定切分策略：枚举root的切分策略，cone内其余op按照通信最小选择（贪心/DP）
  • segment
    • 继续增大粒度：大模型在结构上重复堆叠，可以划分为多个layer。然后通过图分析识别图中关键点（也是cone中的root点），作为间隔点，将模型划分为线性个segment（包含多个cone）
    • 对每个segment都决定切分策略：枚举关键点的切分策略，将cone作为基础块，最小化通信开销，使用ILP solver来获得该segment的切分策略（关键点也就是某个cone的root，不是在上一步就决定好它的拆分了吗，这里需要决定的拆分是怎样的？）
  • all graph
    • 现在graph由近似线性拓扑的segment组成，天然适合DP来解决，以获得全图通信开销最小

all graph

Pipeline strategy

pipeline stage的划分：

  • 要求各个stage计算量均匀，最小化communication section
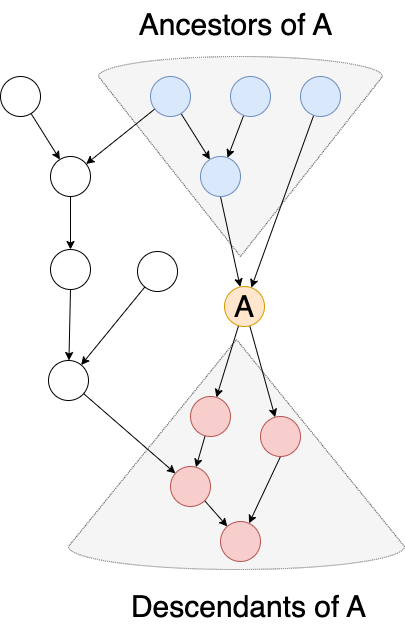
  • 节点的前驱（下图蓝色）和后继关系（下图红色）将作为线性约束来建模ILP问题

pipeline stage

other

只看了auto-distirbuted的技术，其他没关注，感兴趣可以参考看看论文和官方blog 学习

other

MLSys
MLSys Auto Parallelism
This post is licensed under CC BY-NC-SA 4.0 by the author.
Recently Updated
Contents

Triton 编译安装

Triton Survey