最近尝试了一下 Triton-Linalg ，一个开源的工作，支持了几乎所有 triton 原语到 linalg-on-tensor 的下降流程，在这里记录一下自己的学习过程。项目仓库： Triton-Linalg 仓库。

不看长文请调转：浅谈寒武纪开源的Triton-Linalg编译器前端

这将是一篇长文（车轱辘话全集），大该有以下部分，目前还未完工~

介绍（背景、优缺点、和triton-shared的区别）
环境配置 : clone & 编译
测试使用（测试一些例子，简单介绍一下使用）
dialect
- Auxiliar
- LinalgExt
Analysis
Conversion
Pipeline

本文已经更新完成，但是受限于篇幅和个人学识，还请大家带着理性眼光看待，有需要请阅读源码～

本人知识深度有限，还望大家指正~

what’s this

linalg

了解 mlir 的同学一定不陌生 linalg，可以简单地认为是一个胶水层，能表示很多computation、structure信息，起承上启下的作用。

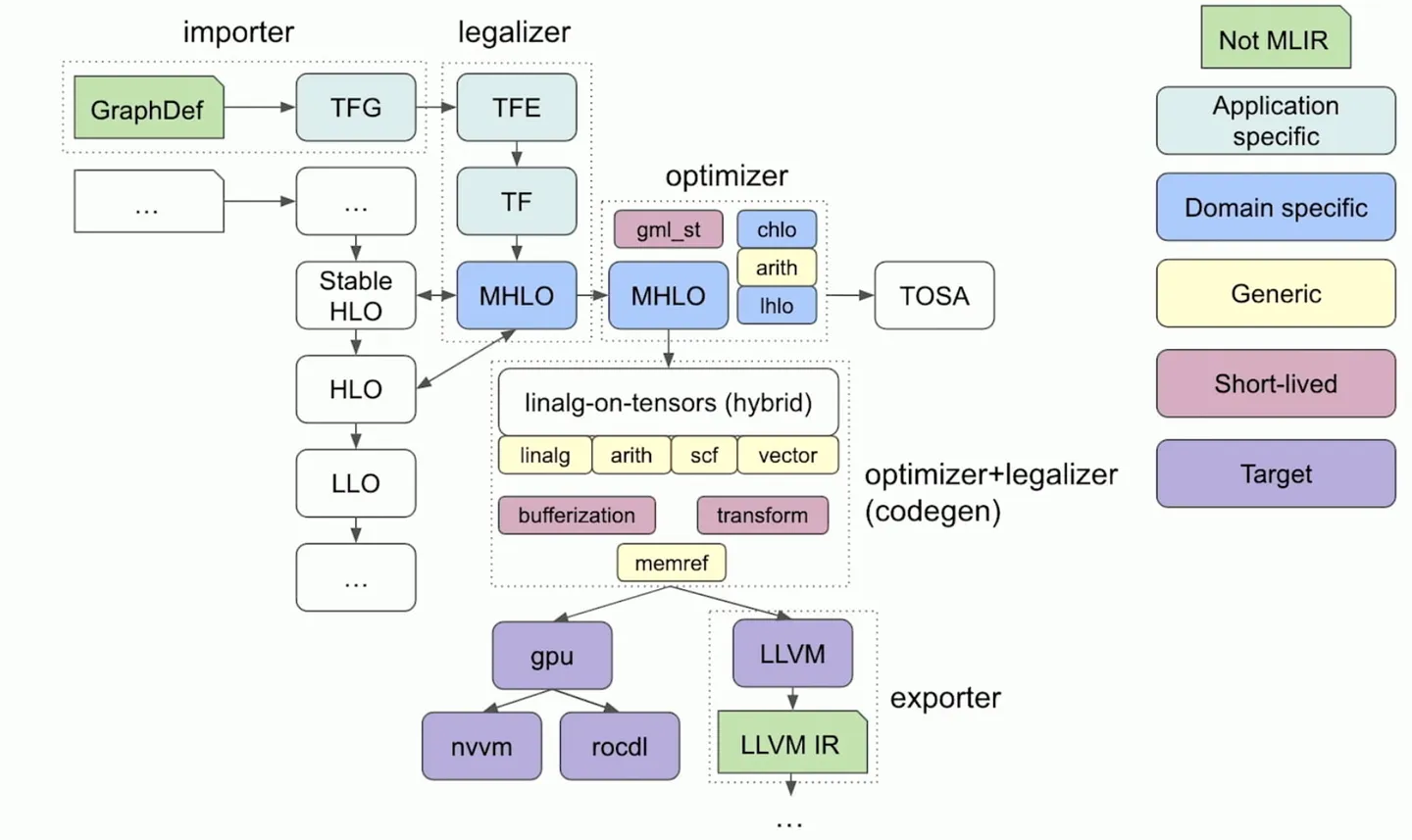
下图是基于mlir的设计compiler时，一些常用的dialect，图源2023 EuroLLVM - MLIR Dialect Design and Composition for Front-End Compilers。

当前从模型到 linalg 的技术路线社区已经比较成熟（例如 model->onnx->stablehlo->linalg，或者翻翻 IREE 的代码），可以说，硬件厂商支持基于mlir的ai compiler的主要工作在 linalg 往下，设计 HWS(HardWare-Special) Dialect。

triton

很多大佬都介绍过了，都写得很好，例如： bbuf大佬的笔记，董鑫大佬关于如何入门的回答

一搜一个不吱声，直接埋头开卷！

简单来说，triton 可以让大家用更少的时间获得较为不错的性能，来验证自己的想法，深受现在学界的喜爱。当然工业界一些很好的 triton 工作了，例如 lightllm中有很多用triton实现的kernel。

triton-linalg

triton-linalg 顾名思义，是为triton(dialect)下降到linalg(dialect)提供了一条可行的路线。如果大家看过 triton 的源码就会发现目前它的下降行为十分直接，一个猛子完成 triton dialect->triton gpu dialect->llvm(见triton conversion)，在这些转换中分布着一些gpu硬件特有的trick保证来codegen出的ir性能不错。

“但是，代价是什么呢” -> 于我而言，代价是需要很多硬件背景知识才能读懂为什么要那么做，以及只能用在 GPU 上，为NV帝国添砖瓦，什么时候才能把价钱打下来

开始“龙场悟道“（自闭）：

那么有没有一种和硬件无关的层级表示 ir 能方便大家读懂且接入自己的硬件呢？ ->

直接从 ttir(triton dialect ir) 接自己的 dialect(类似 TritonGPUDialect)? ->

那万一以后 triton 又不行了，出来一个其他的呢，又适配一遍么？ ->

开摆！（x）看看业界领先经验（√）-> 跟紧 mojo大法师，拥抱 mlir 社区，而 linalg 作为 mlir 社区中很重要的一个中间层。

what can we do with this

triton 重要性： triton 从 pytorch2.0 后已正式作为 inductor 的 gpu 后端，也就是说用户写到的 python 代码会经过 inductor 得到 triton language，然后经过编译后再执行，实现性能提升。接入 triton = 接入 pytorch = 走上人生巅峰 = 给别人埋bug…

感兴趣的同学可以了解下 torch.compile

扩展性： linalg - to - HW special dialect

（借用一下大佬的图，来源见水印）

中间层级优化：trion目前GPU的下降路线过于生硬，可以说是直接一把 conversion，一把下降会导致难以优化中间 IR（例如离散性优化），这对 SIMT 虽然影响不大（每个wrap内的thread执行的指令相同，可能进行Memory-Coalescing，提升访存效率），但是离散地访存行为对 SIMD 的影响无疑是巨大的。

以说是直接一把 conversion，一把下降会导致难以优化中间 IR（例如离散性优化），这对 SIMT 虽然影响不大，但是离散地访存行为对 SIMD 的影响无疑巨大

GPU 中当一个 warp 内多个 thread 访问的地址连续，那么这些访问就可以 coalesce，从而降低全局内存的访问开销。

triton-shared

triton-shared 是 microsoft（巨硬）家实现 triton-to-linalg 的工作（以及实现以CPU作为后端），也扩展了特定的 Dialect。

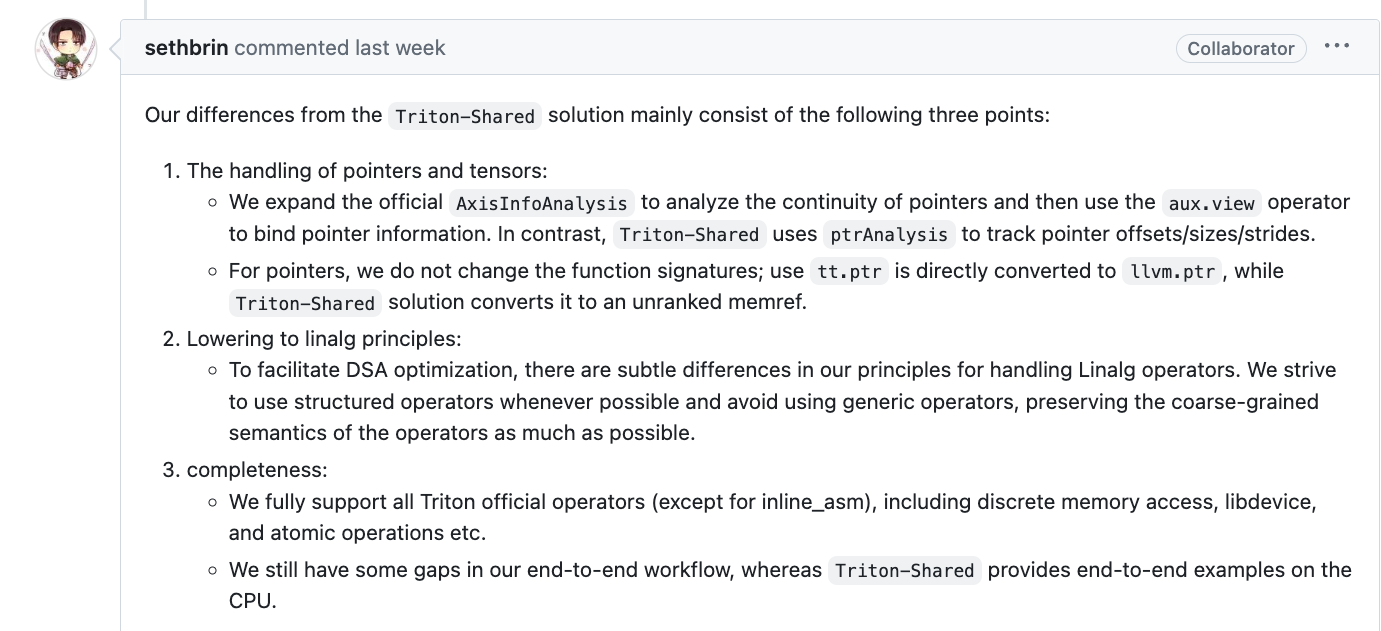
diff with triton-shared

[发现issue中有大哥关于区别的回答，update一下]

支持完整度不同
算子层面，triton-linalg 支持更全面，triton-shared 暂时还没支持 atomic/libdevice 等算子。验证层面，triton-shared 有naive CPU端到端的功能验证支持，而triton-linalg缺少完整端到端功能验证，到 linalg 后的支持需要应用者自己参与，只是提供了轮子。
下降行为不同
triton-linalg 引入了两种新 dialect (LinalgExt和Auxiliary) 来完整算子支持， triton-shared引入了 TritonStructured。以及其他一些算子的下降逻辑不同。

以指针访存(tl.load)的处理为例：

triton-shared: 指针转为 memref<*xf32> -> 通过pointer analysis计算出 strides,shapes,offset，使用 memref.reinterpret_cast 将memref<*xf32>转成数据实际存放的memref -> 通过 memref.copy + bufferization.to_tensor 转成tensor语义下的操作
triton-linalg: 指针会使用llvm.inttoptr 转为 llvm.ptr (和 triton 官方一致)-> 通过AxisInfoAnalysis计算出 strides,shapes,offset(实际是分析出访存的连续性)，使用 aux.view 将llvm.ptr转成数据实际存放的memref -> 通过 bufferization.to_tensor 转为tensor语义下的操作，再使用 linalg.copy(连续访存) 或 linalg_ext.gather(离散访存) 来获取数据

环境配置

clone

  
export TRITON_PLUGIN_DIRS=$(pwd)/triton-linalg
git clone --recurse-submodules https://github.com/Cambricon/triton-linalg.git
cd triton-linalg/triton

python 环境

  
conda create --name triton_env python=3.10 # 版本要大于等于3.8
conda activate triton_env
conda install numpy matplotlib pybind11 lit pytest isort pandas tabulate scipy flake8 autopep8
conda install pytorch torchvision # 我也不确定需不需要，反正cpu的不大

相关工具按照 Triton-Linalg README 内容进行环境配置和编译

由于我是在 macOS 上编译，所以直接通过 brew 安装了相关工具

  
brew install cmake ninja-build ccache clang lld
conda install pytest-xdist cython # 记得要装cython

正常在 linux 下使用 apt-get 安装相关工具链即可

  
python3 -m pip install --upgrade pip
python3 -m pip install cmake ninja pytest-xdist cython # 这样装的cmake版本目前是3.26
sudo apt-get update -y
sudo apt-get install -y ccache clang lld

编译

注意，编译的时候需要进入 triton-linalg/triton 文件夹

  
# macos中lld是不能work的，所以不要添加相关的编译选项，在linux下就没问题
#TRITON_BUILD_WITH_CLANG_LLD=true TRITON_BUILD_WITH_CCACHE=true pip install -e python --no-build-isolation -vvv
pip3 install -e python --no-build-isolation

note: 我用 macOS 编译的时候遇见编译报错 “找不到 bits/std_abs.h”。翻了一下 macOS (/Library/Developer/CommandLineTools/SDKs/MacOSX14.4.sdk/usr/include/)的clang确实没有。只需要把 lib/Dialect/Triton/Transforms/InferAxisInfoInterfaceImpl.cpp 中的 bits/std_abs.h 换成 stdlib.h 即正常编译

编译完成：

编译好的 triton-linalg-opt 在 triton-linalg/triton/python/build/{current_cmake_version}/third_party/triton_linalg/bin/triton-linalg-opt ，如果没有找到，说明没有设置环境变量 export TRITON_PLUGIN_DIRS=$(pwd)/triton-linalg 没有配置对，重新设置下再运行一次编译命令即可。

测试使用

差生文具多

为了方便索引，编译完成后在 triton-linalg/triton/python/build/ 目录下有一个 compile_commands.json，将其 cp 到 triton-linalg目录下，再在 vscode 中简单地配置下 ctrl + p 输入 clangd，先点击下载language server；然后加 settings.json , ctrl + p → ‘> 打开工作区设置json’

  
{
    "clangd.arguments": [
        "--header-insertion=never",
        "--compile-commands-dir=${workspaceFolder}/",
        "--query-driver=**",
    ]
}

加个环境变量，方便使用

  
export PATH=xxx/triton-linalg/triton/python/build/{current_cmake_version}/third_party/triton_linalg/bin:$PATH
# triton-opt 在 xxx/triton-linalg/triton/python/build/{current_cmake_version}/bin

打印ir的方法

在kernel后增加

  
    grid = lambda META: (triton.cdiv(M, META['BLOCK_SIZE_M']) * triton.cdiv(N, META['BLOCK_SIZE_N']), )
    kernel = matmul_kernel[grid](
        a, b, c,  #
        M, N, K,  #
        a.stride(0), a.stride(1),  #
        b.stride(0), b.stride(1),  #
        c.stride(0), c.stride(1),  #
        ACTIVATION=activation  #
    )
    print(kernel.asm['ttir'])
    print(kernel.asm['ttgir'])
    print(kernel.asm['llir'])
    print(kernel.asm['ptx'])

运行python文件时加上 MLIR_ENABLE_DUMP=1

dumps the IR before every MLIR pass Triton runs

一窥ttir

triton-llinalg-opt 真正能吃下的输入并不是 python，而是 ttir (triton ir)，可以理解成一般性流程是 python -> ttit -> linalg / gpu dialect -> llvm

以 tutorials/03-matrix-multiplication.py 为例，输入：

  
def matmul_kernel(
        # Pointers to matrices
        a_ptr, b_ptr, c_ptr,
        # Matrix dimensions
        M, N, K,
        # The stride variables represent how much to increase the ptr by when moving by 1
        # element in a particular dimension. E.g. `stride_am` is how much to increase `a_ptr`
        # by to get the element one row down (A has M rows).
        stride_am, stride_ak,  #
        stride_bk, stride_bn,  #
        stride_cm, stride_cn,
        # Meta-parameters
        BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr, BLOCK_SIZE_K: tl.constexpr,  #
        GROUP_SIZE_M: tl.constexpr,  #
        ACTIVATION: tl.constexpr  #
):
    pid = tl.program_id(axis=0)
    num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
    num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
    num_pid_in_group = GROUP_SIZE_M * num_pid_n
    group_id = pid // num_pid_in_group
    first_pid_m = group_id * GROUP_SIZE_M
    group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
    pid_m = first_pid_m + ((pid % num_pid_in_group) % group_size_m)
    pid_n = (pid % num_pid_in_group) // group_size_m

    offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
    offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
    offs_k = tl.arange(0, BLOCK_SIZE_K)
    a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
    b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)

    accumulator = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
    for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)):
        a = tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
        b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
        accumulator = tl.dot(a, b, accumulator)
        a_ptrs += BLOCK_SIZE_K * stride_ak
        b_ptrs += BLOCK_SIZE_K * stride_bk

    if ACTIVATION == "leaky_relu":
        accumulator = leaky_relu(accumulator)
    c = accumulator.to(tl.float16)

    offs_cm = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
    offs_cn = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
    c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
    c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
    tl.store(c_ptrs, c, mask=c_mask)

输出 ttir 时主要下降为 tt.ops + arith.ops，具体参考 triton/python/triton/language/semantic.py

// 这个保存为 matmul.ttir
module {
  tt.func public @matmul_kernel(%arg0: !tt.ptr<f16>, %arg1: !tt.ptr<f16>, %arg2: !tt.ptr<f16>, %arg3: i32, %arg4: i32, %arg5: i32, %arg6: i32, %arg7: i32, %arg8: i32) {
    // blockarg对应：（都是根据ir推出来的）
    // %arg0: a_ptr, %arg1: b_ptr, %arg2: c_ptr
    // %arg3: M, %arg4: N, %arg5: K
    // %arg6: stride_am, %arg7: stride_bk, %arg8: stride_cm
    // 推出： stride_ak = 1, stride_bn = 1, stride_cn = 1

    // 常量部分，有些是这次 tuning 选择的 config 中的 超参数（tl.constexpr）具体值
    %cst = arith.constant dense<0.000000e+00> : tensor<128x64xf16>
    %cst_0 = arith.constant dense<0.000000e+00> : tensor<64x64xf16>
    %c63_i32 = arith.constant 63 : i32
    %c127_i32 = arith.constant 127 : i32
    %c1_i32 = arith.constant 1 : i32
    %c0_i32 = arith.constant 0 : i32
    %cst_1 = arith.constant dense<64> : tensor<128x64xi32>
    %cst_2 = arith.constant dense<0.000000e+00> : tensor<128x64xf32>
    %c64_i32 = arith.constant 64 : i32
    %c128_i32 = arith.constant 128 : i32
    %c8_i32 = arith.constant 8 : i32

    // pid = tl.program_id(axis=0)
    %0 = tt.get_program_id x : i32

    // %arg3: M, %arg4: N
    // num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
    // (x + (2^n - 1)) / 2^n -> 实现向上取整
    // 这次 tuning config的 BLOCK_SIZE_M 是 128
    %1 = arith.addi %arg3, %c127_i32 : i32
    %2 = arith.divsi %1, %c128_i32 : i32

    // num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
    // 这次 tuning config的 BLOCK_SIZE_N 是 64
    %3 = arith.addi %arg4, %c63_i32 : i32
    %4 = arith.divsi %3, %c64_i32 : i32

    // num_pid_in_group = GROUP_SIZE_M * num_pid_n
    // 这次 tuning config的 GROUP_SIZE_M 是 8
    %5 = arith.muli %4, %c8_i32 : i32

    // group_id = pid // num_pid_in_group
    %6 = arith.divsi %0, %5 : i32

    // frist_pid_m = group_id * GROUP_SIZE_M
    %7 = arith.muli %6, %c8_i32 : i32

    // group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
    %8 = arith.subi %2, %7 : i32
    %9 = arith.minsi %8, %c8_i32 : i32

    // pid_m = first_pid_m + ((pid % num_pid_in_group) % group_size_m)
    // %11 = pid % group_size_m + first_pid_m 这里对不上 pid_m 的计算
    %10 = arith.remsi %0, %9 : i32
    %11 = arith.addi %7, %10 : i32

    // pid_n = (pid % num_pid_in_group) // group_size_m
    %12 = arith.remsi %0, %5 : i32
    %13 = arith.divsi %12, %9 : i32

    // offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
    %14 = arith.muli %11, %c128_i32 : i32
    // %15 = tl.arange(0, BLOCK_SIZE_M)
    %15 = tt.make_range {end = 128 : i32, start = 0 : i32} : tensor<128xi32>
    %16 = tt.splat %14 : i32 -> tensor<128xi32>
    // %17 = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
    %17 = arith.addi %16, %15 : tensor<128xi32>
    %18 = tt.splat %arg3 : i32 -> tensor<128xi32>
    %19 = arith.remsi %17, %18 : tensor<128xi32>

    // offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
    %20 = arith.muli %13, %c64_i32 : i32
    // 因为BLOCK_SIZE_K = BLOCK_SIZE_N， 所以复用了make_range
    // offs_k = tl.arange(0, BLOCK_SIZE_K) = tl.arange(0, BLOCK_SIZE_N)
    %21 = tt.make_range {end = 64 : i32, start = 0 : i32} : tensor<64xi32>
    %22 = tt.splat %20 : i32 -> tensor<64xi32>
    // %23 = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
    %23 = arith.addi %22, %21 : tensor<64xi32>
    %24 = tt.splat %arg4 : i32 -> tensor<64xi32>
    %25 = arith.remsi %23, %24 : tensor<64xi32>

    // a_ptrs = a_ptr + (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
    %26 = tt.expand_dims %19 {axis = 1 : i32} : tensor<128xi32> -> tensor<128x1xi32>
    // %arg6: stride_am, splat 成同shape tensor，然后乘
    %27 = tt.splat %arg6 : i32 -> tensor<128x1xi32>
    %28 = arith.muli %26, %27 : tensor<128x1xi32>
    // %21 = offs_k = tl.arange(0, BLOCK_SIZE_K)
    %29 = tt.expand_dims %21 {axis = 0 : i32} : tensor<64xi32> -> tensor<1x64xi32>
    // 这里是 stride_ak = 1
    %30 = tt.broadcast %28 : tensor<128x1xi32> -> tensor<128x64xi32>
    %31 = tt.broadcast %29 : tensor<1x64xi32> -> tensor<128x64xi32>
    %32 = arith.addi %30, %31 : tensor<128x64xi32>
    // 把 a_ptr splat 成 对应 shape
    %33 = tt.splat %arg0 : !tt.ptr<f16> -> tensor<128x64x!tt.ptr<f16>>
    %34 = tt.addptr %33, %32 : tensor<128x64x!tt.ptr<f16>>, tensor<128x64xi32>

    // b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
    %35 = tt.expand_dims %21 {axis = 1 : i32} : tensor<64xi32> -> tensor<64x1xi32>
    // %arg7: stride_bk
    %36 = tt.splat %arg7 : i32 -> tensor<64x1xi32>
    %37 = arith.muli %35, %36 : tensor<64x1xi32>
    %38 = tt.expand_dims %25 {axis = 0 : i32} : tensor<64xi32> -> tensor<1x64xi32>
    %39 = tt.broadcast %37 : tensor<64x1xi32> -> tensor<64x64xi32>
    // 这里是 stride_bn = 1
    %40 = tt.broadcast %38 : tensor<1x64xi32> -> tensor<64x64xi32>
    %41 = arith.addi %39, %40 : tensor<64x64xi32>
    %42 = tt.splat %arg1 : !tt.ptr<f16> -> tensor<64x64x!tt.ptr<f16>>
    %43 = tt.addptr %42, %41 : tensor<64x64x!tt.ptr<f16>>, tensor<64x64xi32>

    // scf.for 循环上界 tl.cdiv(K, BLOCK_SIZE_K)
    // %arg5: K, 这次 tuning config的 BLOCK_SIZE_K 是 64
    %44 = arith.addi %arg5, %c63_i32 : i32
    %45 = arith.divsi %44, %c64_i32 : i32

    // %47 = BLOCK_SIZE_K * stride_bk
    %46 = arith.muli %arg7, %c64_i32 : i32
    %47 = tt.splat %46 : i32 -> tensor<64x64xi32>

    // for k in range(0, tl.cdiv(K, BLOCK_SIZE_K)), %arg9即k
    // 每一轮都在改变：%arg10: accumulator, %arg11: %a_ptrs, %12: %b_ptrs
    %48:3 = scf.for %arg9 = %c0_i32 to %45 step %c1_i32 iter_args(%arg10 = %cst_2, %arg11 = %34, %arg12 = %43) -> (tensor<128x64xf32>, tensor<128x64x!tt.ptr<f16>>, tensor<64x64x!tt.ptr<f16>>)  : i32 {
      // %67 = K - k * BLOCK_SIZE_K
      %66 = arith.muli %arg9, %c64_i32 : i32
      %67 = arith.subi %arg5, %66 : i32

      // a_mask计算 splat 后和 offsets_k 比较
      %68 = tt.splat %67 : i32 -> tensor<1x64xi32>
      %69 = arith.cmpi slt, %29, %68 : tensor<1x64xi32>
      %70 = tt.broadcast %69 : tensor<1x64xi1> -> tensor<128x64xi1>
      // tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
      %71 = tt.load %arg11, %70, %cst : tensor<128x64x!tt.ptr<f16>>

      // b_mask计算 splat 后和 offsets_k 比较
      %72 = tt.splat %67 : i32 -> tensor<64x1xi32>
      %73 = arith.cmpi slt, %35, %72 : tensor<64x1xi32>
      %74 = tt.broadcast %73 : tensor<64x1xi1> -> tensor<64x64xi1>
      // b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
      %75 = tt.load %arg12, %74, %cst_0 : tensor<64x64x!tt.ptr<f16>>

      // accumulator = tl.dot(a, b, accumulator)
      %76 = tt.dot %71, %75, %arg10, inputPrecision = tf32 : tensor<128x64xf16> * tensor<64x64xf16> -> tensor<128x64xf32>

      // a_ptrs += BLOCK_SIZE_K * stride_ak
      // 前面的代码推论出 stride_ak = 1，%cst_1 = arith.constant dense<64> : tensor<128x64xi32>，相当于 1x64(BLOCK_SIZE_K)
      %77 = tt.addptr %arg11, %cst_1 : tensor<128x64x!tt.ptr<f16>>, tensor<128x64xi32>

      // b_ptrs += BLOCK_SIZE_K * stride_bk
      %78 = tt.addptr %arg12, %47 : tensor<64x64x!tt.ptr<f16>>, tensor<64x64xi32>

      // 返回，给下次循环作为blockarg
      scf.yield %76, %77, %78 : tensor<128x64xf32>, tensor<128x64x!tt.ptr<f16>>, tensor<64x64x!tt.ptr<f16>>
    }

    // c = accumulator.to(tl.float16)
    %49 = arith.truncf %48#0 : tensor<128x64xf32> to tensor<128x64xf16>

    // c_ptrs = c_ptr + stride_cm * offs_cm[:, None] + stride_cn * offs_cn[None, :]
    // offs_cm = %17 = pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)
    %50 = tt.expand_dims %17 {axis = 1 : i32} : tensor<128xi32> -> tensor<128x1xi32>
    // %arg8: stride_cm, %52 = stride_cm * offs_cm[:, None]
    %51 = tt.splat %arg8 : i32 -> tensor<128x1xi32>
    %52 = arith.muli %51, %50 : tensor<128x1xi32>
    // %arg2: c_ptr
    %53 = tt.splat %arg2 : !tt.ptr<f16> -> tensor<128x1x!tt.ptr<f16>>
    %54 = tt.addptr %53, %52 : tensor<128x1x!tt.ptr<f16>>, tensor<128x1xi32>
    // offs_cn = %23 = pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
    // 推断出 stride_cn = 1
    %55 = tt.expand_dims %23 {axis = 0 : i32} : tensor<64xi32> -> tensor<1x64xi32>
    %56 = tt.broadcast %54 : tensor<128x1x!tt.ptr<f16>> -> tensor<128x64x!tt.ptr<f16>>
    %57 = tt.broadcast %55 : tensor<1x64xi32> -> tensor<128x64xi32>
    %58 = tt.addptr %56, %57 : tensor<128x64x!tt.ptr<f16>>, tensor<128x64xi32>

    // c_mask = (offs_cm[:, None] < M) & (offs_cn[None, :] < N)
    %59 = tt.splat %arg3 : i32 -> tensor<128x1xi32>
    %60 = arith.cmpi slt, %50, %59 : tensor<128x1xi32>
    %61 = tt.splat %arg4 : i32 -> tensor<1x64xi32>
    %62 = arith.cmpi slt, %55, %61 : tensor<1x64xi32>
    %63 = tt.broadcast %60 : tensor<128x1xi1> -> tensor<128x64xi1>
    %64 = tt.broadcast %62 : tensor<1x64xi1> -> tensor<128x64xi1>
    %65 = arith.andi %63, %64 : tensor<128x64xi1>

    // tl.store(c_ptrs, c, mask=c_mask)
    tt.store %58, %49, %65 : tensor<128x64x!tt.ptr<f16>>
    tt.return
  }
}

瞅瞅linalg

终于，linalg登场了，看懂这一步的ir，才好理解triton-linalg的主要工作。我们继续lower到linalg上，一眼 tensor + linalg + bufferization，以及两个该仓库自定义的dialect (aux + linalg_ext)，后节会讲讲。

总结一下，在这段ir中（根据连续性情况，load/store指令会下降出不同的结果）有以下对应关系：

ttir	linalg
arith.ops 标量计算	arith.ops 标量计算
arith.constant表示的tensor	linalg.fill
tt.make_range	linalg_ext.make_range
arith.ops tensor计算	linalg.map{arith.ops}
tt.broadcast	linalg.broadcast
tt.addptr	linalg.map{arith.muli+arith.addi}
tt.dot	linalg.matmul
可变mask中的信息 mul + sub + cmp	可变mask中的信息 mul + sub + fill + pad
tt.load	llvm.inttoptr + aux.view + bufferization.to_tensor + linalg_ext.gather
tt.store	llvm.inttoptr + aux.view + bufferization.materialize_in_destination

对ptr进行load/store时，通过llvm.inttoptr + aux.view转为来对memref的操作。（现在只是对比ir的情况获得的上表，具体还要看 TritonToLinalg.cpp 中的代码，咱之后再分析）

ExtractLikeMoveBackwardPass 和 Canonicalizer 导致 -triton-to-linalg输出的结果比较难理解，所以在直接-triton-to-linalg -mlir-print-ir-after-all 看 TritonToLinalgPass 结束后的ir。下面这段ir还没有经过 cse 和 canonicalize，所以显得比较冗余。

// triton-linalg-opt -triton-to-linalg matmul.ttir
#map = affine_map<(d0, d1)[s0, s1] -> (d0 * s1 + s0 + d1)>
module {
  func.func @matmul_kernel(%arg0: i64, %arg1: i64, %arg2: i64, %arg3: i32, %arg4: i32, %arg5: i32, %arg6: i32, %arg7: i32, %arg8: i32) {
    %cst = arith.constant 0.000000e+00 : f16
    %0 = tensor.empty() : tensor<128x64xf16>
    // arith.constant 表示的tensor下降为 linalg.fill
    %1 = linalg.fill ins(%cst : f16) outs(%0 : tensor<128x64xf16>) -> tensor<128x64xf16>
    %cst_0 = arith.constant 0.000000e+00 : f16
    %2 = tensor.empty() : tensor<64x64xf16>
    %3 = linalg.fill ins(%cst_0 : f16) outs(%2 : tensor<64x64xf16>) -> tensor<64x64xf16>
    %c63_i32 = arith.constant 63 : i32
    %c127_i32 = arith.constant 127 : i32
    %c1_i32 = arith.constant 1 : i32
    %c0_i32 = arith.constant 0 : i32
    %c64_i32 = arith.constant 64 : i32
    %4 = tensor.empty() : tensor<128x64xi32>
    %5 = linalg.fill ins(%c64_i32 : i32) outs(%4 : tensor<128x64xi32>) -> tensor<128x64xi32>
    %cst_1 = arith.constant 0.000000e+00 : f32
    %6 = tensor.empty() : tensor<128x64xf32>
    %7 = linalg.fill ins(%cst_1 : f32) outs(%6 : tensor<128x64xf32>) -> tensor<128x64xf32>
    %c64_i32_2 = arith.constant 64 : i32
    %c128_i32 = arith.constant 128 : i32
    %c8_i32 = arith.constant 8 : i32

    // tt.get_program_id 在目前还没该变，后续应该类似gpu的行为，转为(x, y, z)来表示任务id
    %8 = tt.get_program_id x : i32
    // %arg3: M, %arg4: N
    // num_pid_m = tl.cdiv(M, BLOCK_SIZE_M)
    %9 = arith.addi %arg3, %c127_i32 : i32
    %10 = arith.divsi %9, %c128_i32 : i32
    // num_pid_n = tl.cdiv(N, BLOCK_SIZE_N)
    %11 = arith.addi %arg4, %c63_i32 : i32
    %12 = arith.divsi %11, %c64_i32_2 : i32
    // num_pid_in_group = GROUP_SIZE_M  * num_pid_n
    %13 = arith.muli %12, %c8_i32 : i32
    // group_id = pid // num_pid_in_group
    %14 = arith.divsi %8, %13 : i32
    // frist_pid_m = group_id * GROUP_SIZE_M
    %15 = arith.muli %14, %c8_i32 : i32
    // group_size_m = min(num_pid_m - first_pid_m, GROUP_SIZE_M)
    %16 = arith.subi %10, %15 : i32
    %17 = arith.minsi %16, %c8_i32 : i32
    // pid_m = first_pid_m + ((pid % num_pid_in_group) % group_size_m)
    %18 = arith.remsi %8, %17 : i32
    %19 = arith.addi %15, %18 : i32
    // pid_n = (pid % num_pid_in_group) // group_size_m
    %20 = arith.remsi %8, %13 : i32
    %21 = arith.divsi %20, %17 : i32
    %22 = arith.muli %19, %c128_i32 : i32

    // offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
    %23 = tensor.empty() : tensor<128xi32>
    %c0_i32_3 = arith.constant 0 : i32
    %c128_i32_4 = arith.constant 128 : i32
    // tt.make_range -> linalg_ext.make_range
    %24 = linalg_ext.make_range {operandSegmentSizes = array<i32: 2, 1>} ins(%c0_i32_3, %c128_i32_4 : i32, i32) outs(%23 : tensor<128xi32>) -> tensor<128xi32>
    %25 = tensor.empty() : tensor<128xi32>
    // tt.splat -> linalg.fill
    %26 = linalg.fill ins(%22 : i32) outs(%25 : tensor<128xi32>) -> tensor<128xi32>
    %27 = tensor.empty() : tensor<128xi32>
    // arith.ops+tensor -> linalg.map{arith.ops}
    %mapped = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%26, %24 : tensor<128xi32>, tensor<128xi32>) outs(%27 : tensor<128xi32>)
    %28 = tensor.empty() : tensor<128xi32>
    %29 = linalg.fill ins(%arg3 : i32) outs(%28 : tensor<128xi32>) -> tensor<128xi32>
    %30 = tensor.empty() : tensor<128xi32>
    %mapped_5 = linalg.map { arith.remsi } ins(%mapped, %29 : tensor<128xi32>, tensor<128xi32>) outs(%30 : tensor<128xi32>)

    // offs_bn = (pid_n * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)) % N
    %31 = arith.muli %21, %c64_i32_2 : i32
    %32 = tensor.empty() : tensor<64xi32>
    %c0_i32_6 = arith.constant 0 : i32
    %c64_i32_7 = arith.constant 64 : i32
    // offs_k = tl.arange(0, BLOCK_SIZE_K) = tl.arange(0, BLOCK_SIZE_N)
    %33 = linalg_ext.make_range {operandSegmentSizes = array<i32: 2, 1>} ins(%c0_i32_6, %c64_i32_7 : i32, i32) outs(%32 : tensor<64xi32>) -> tensor<64xi32>
    %34 = tensor.empty() : tensor<64xi32>
    %35 = linalg.fill ins(%31 : i32) outs(%34 : tensor<64xi32>) -> tensor<64xi32>
    %36 = tensor.empty() : tensor<64xi32>
    %mapped_8 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%35, %33 : tensor<64xi32>, tensor<64xi32>) outs(%36 : tensor<64xi32>)
    %37 = tensor.empty() : tensor<64xi32>
    %38 = linalg.fill ins(%arg4 : i32) outs(%37 : tensor<64xi32>) -> tensor<64xi32>
    %39 = tensor.empty() : tensor<64xi32>
    %mapped_9 = linalg.map { arith.remsi } ins(%mapped_8, %38 : tensor<64xi32>, tensor<64xi32>) outs(%39 : tensor<64xi32>)

    // mapped_14 = (offs_am[:, None] * stride_am + offs_k[None, :] * stride_ak)
    // tt.expaned_dims -> tensor.expand_shape
    %expanded = tensor.expand_shape %mapped_5 [[0, 1]] : tensor<128xi32> into tensor<128x1xi32>
    %40 = tensor.empty() : tensor<128x1xi32>
    %41 = linalg.fill ins(%arg6 : i32) outs(%40 : tensor<128x1xi32>) -> tensor<128x1xi32>
    %42 = tensor.empty() : tensor<128x1xi32>
    %mapped_10 = linalg.map { arith.muli {overflowFlags = #arith.overflow<none>} } ins(%expanded, %41 : tensor<128x1xi32>, tensor<128x1xi32>) outs(%42 : tensor<128x1xi32>)
    %expanded_11 = tensor.expand_shape %33 [[0, 1]] : tensor<64xi32> into tensor<1x64xi32>
    // tt.broadcast -> tensor.collapse_shape + linalg.broadcast
    %collapsed = tensor.collapse_shape %mapped_10 [[0, 1]] : tensor<128x1xi32> into tensor<128xi32>
    %43 = tensor.empty() : tensor<128x64xi32>
    %broadcasted = linalg.broadcast ins(%collapsed : tensor<128xi32>) outs(%43 : tensor<128x64xi32>) dimensions = [1]
    %collapsed_12 = tensor.collapse_shape %expanded_11 [[0, 1]] : tensor<1x64xi32> into tensor<64xi32>
    %44 = tensor.empty() : tensor<128x64xi32>
    %broadcasted_13 = linalg.broadcast ins(%collapsed_12 : tensor<64xi32>) outs(%44 : tensor<128x64xi32>) dimensions = [0]
    %45 = tensor.empty() : tensor<128x64xi32>
    %mapped_14 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%broadcasted, %broadcasted_13 : tensor<128x64xi32>, tensor<128x64xi32>) outs(%45 : tensor<128x64xi32>)

    // mapped_22 = (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
    %expanded_15 = tensor.expand_shape %33 [[0, 1]] : tensor<64xi32> into tensor<64x1xi32>
    %46 = tensor.empty() : tensor<64x1xi32>
    %47 = linalg.fill ins(%arg7 : i32) outs(%46 : tensor<64x1xi32>) -> tensor<64x1xi32>
    %48 = tensor.empty() : tensor<64x1xi32>
    %mapped_16 = linalg.map { arith.muli {overflowFlags = #arith.overflow<none>} } ins(%expanded_15, %47 : tensor<64x1xi32>, tensor<64x1xi32>) outs(%48 : tensor<64x1xi32>)
    %expanded_17 = tensor.expand_shape %mapped_9 [[0, 1]] : tensor<64xi32> into tensor<1x64xi32>
    %collapsed_18 = tensor.collapse_shape %mapped_16 [[0, 1]] : tensor<64x1xi32> into tensor<64xi32>
    %49 = tensor.empty() : tensor<64x64xi32>
    %broadcasted_19 = linalg.broadcast ins(%collapsed_18 : tensor<64xi32>) outs(%49 : tensor<64x64xi32>) dimensions = [1]
    %collapsed_20 = tensor.collapse_shape %expanded_17 [[0, 1]] : tensor<1x64xi32> into tensor<64xi32>
    %50 = tensor.empty() : tensor<64x64xi32>
    %broadcasted_21 = linalg.broadcast ins(%collapsed_20 : tensor<64xi32>) outs(%50 : tensor<64x64xi32>) dimensions = [0]
    %51 = tensor.empty() : tensor<64x64xi32>
    %mapped_22 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%broadcasted_19, %broadcasted_21 : tensor<64x64xi32>, tensor<64x64xi32>) outs(%51 : tensor<64x64xi32>)

    // scf.for 循环上界 tl.cdiv(K, BLOCK_SIZE_K)
    %52 = arith.addi %arg5, %c63_i32 : i32
    %53 = arith.divsi %52, %c64_i32_2 : i32
    %54 = arith.muli %arg7, %c64_i32_2 : i32
    %55 = tensor.empty() : tensor<64x64xi32>
    %56 = linalg.fill ins(%54 : i32) outs(%55 : tensor<64x64xi32>) -> tensor<64x64xi32>
    %57:3 = scf.for %arg9 = %c0_i32 to %53 step %c1_i32 iter_args(%arg10 = %7, %arg11 = %mapped_14, %arg12 = %mapped_22) -> (tensor<128x64xf32>, tensor<128x64xi32>, tensor<64x64xi32>)  : i32 {
      // 计算 b_ptrs
      // %arg12 第一轮是 (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
      // 之后会被更新 %arg12 += BLOCk * stride_ak，保证 b_ptrs 的变化
      %126 = tensor.empty() : tensor<64x64xi64>
      %127 = linalg.fill ins(%arg1 : i64) outs(%126 : tensor<64x64xi64>) -> tensor<64x64xi64>
      %128 = tensor.empty() : tensor<64x64xi64>
      // tt.addptr -> linalg.map{arith.addi}
      %mapped_69 = linalg.map ins(%127, %arg12 : tensor<64x64xi64>, tensor<64x64xi32>) outs(%128 : tensor<64x64xi64>)
        (%in: i64, %in_117: i32) {
          %179 = arith.extsi %in_117 : i32 to i64
          %c2_i64 = arith.constant 2 : i64
          %180 = arith.muli %179, %c2_i64 : i64
          %181 = arith.addi %in, %180 : i64
          linalg.yield %181 : i64
        }

      // 计算 a_ptrs
      %129 = tensor.empty() : tensor<128x64xi64>
      %130 = linalg.fill ins(%arg0 : i64) outs(%129 : tensor<128x64xi64>) -> tensor<128x64xi64>
      %131 = tensor.empty() : tensor<128x64xi64>
      %mapped_70 = linalg.map ins(%130, %arg11 : tensor<128x64xi64>, tensor<128x64xi32>) outs(%131 : tensor<128x64xi64>)
        (%in: i64, %in_117: i32) {
          %179 = arith.extsi %in_117 : i32 to i64
          %c2_i64 = arith.constant 2 : i64
          %180 = arith.muli %179, %c2_i64 : i64
          %181 = arith.addi %in, %180 : i64
          linalg.yield %181 : i64
        }

      // K - k * BLOCK_SIZE_K
      %132 = arith.muli %arg9, %c64_i32_2 : i32
      %133 = arith.subi %arg5, %132 : i32
      %134 = tensor.empty() : tensor<1x64xi32>
      %135 = linalg.fill ins(%133 : i32) outs(%134 : tensor<1x64xi32>) -> tensor<1x64xi32>
      %136 = arith.index_cast %133 : i32 to index
      %c0_71 = arith.constant 0 : index
      // mask，当k满足%137>0时，为true；反之为false
      %137 = arith.maxsi %136, %c0_71 : index
      %c64_72 = arith.constant 64 : index
      // 保证索引小于BLOCK_SIZE_K
      %138 = arith.minsi %c64_72, %137 : index
      %139 = tensor.empty(%138) : tensor<1x?xi1>
      %true_73 = arith.constant true
      %140 = linalg.fill ins(%true_73 : i1) outs(%139 : tensor<1x?xi1>) -> tensor<1x?xi1>
      %false_74 = arith.constant false
      %141 = tensor.empty() : tensor<1x64xi1>
      %c0_75 = arith.constant 0 : index
      %dim_76 = tensor.dim %141, %c0_75 : tensor<1x64xi1>
      %c0_77 = arith.constant 0 : index
      %c1_78 = arith.constant 1 : index
      %142 = arith.addi %c0_77, %c1_78 : index
      %143 = arith.subi %dim_76, %142 : index
      %c1_79 = arith.constant 1 : index
      %dim_80 = tensor.dim %141, %c1_79 : tensor<1x64xi1>
      %c0_81 = arith.constant 0 : index
      %144 = arith.addi %c0_81, %138 : index
      %145 = arith.subi %dim_80, %144 : index
      // mask的信息: minsi + maxsi -> pad -> broadcasted，然后作为 linalg_ext.gather的mask输入
      %146 = linalg_ext.pad ins(%140 : tensor<1x?xi1>) outs(%141 : tensor<1x64xi1>) pvalue(%false_74 : i1) low = [%c0_77, %c0_81] high = [%143, %145] {
      ^bb0(%arg13: i1):
        linalg_ext.yield %arg13 : i1
      } -> tensor<1x64xi1>
      // tt.broadcast -> tensor.collapse_shape + linalg.broadcast
      %collapsed_82 = tensor.collapse_shape %146 [[0, 1]] : tensor<1x64xi1> into tensor<64xi1>
      %147 = tensor.empty() : tensor<128x64xi1>
      %broadcasted_83 = linalg.broadcast ins(%collapsed_82 : tensor<64xi1>) outs(%147 : tensor<128x64xi1>) dimensions = [0]

      // tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
      %c0_i32_84 = arith.constant 0 : i32
      %c0_i32_85 = arith.constant 0 : i32
      %148 = tensor.empty() : tensor<128x64xi32>
      %149 = linalg.fill ins(%c0_i32_85 : i32) outs(%148 : tensor<128x64xi32>) -> tensor<128x64xi32>
      %150 = tensor.empty() : tensor<128x64xi32>
      // layout + 0，感觉没啥意义的计算
      %mapped_86 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%arg11, %149 : tensor<128x64xi32>, tensor<128x64xi32>) outs(%150 : tensor<128x64xi32>)
      // a_ptr -> !llvm.ptr
      %151 = llvm.inttoptr %arg0 : i64 to !llvm.ptr
      // aux.view 从地址(%151是a_ptr)中获得一个无穷大的memref，然后使用bufferization.to_tensor转为tensor来计算
      %view_memref_87 = aux.view %151 to offset: [0], sizes: [9223372036854775807], strides: [1] : !llvm.ptr to memref<9223372036854775807xf16>
      %152 = bufferization.to_tensor %view_memref_87 restrict writable : memref<9223372036854775807xf16>
      %collapsed_88 = tensor.collapse_shape %1 [[0, 1]] : tensor<128x64xf16> into tensor<8192xf16>
      %expanded_89 = tensor.expand_shape %collapsed_88 [[0, 1]] : tensor<8192xf16> into tensor<8192x1xf16>
      %collapsed_90 = tensor.collapse_shape %mapped_86 [[0, 1]] : tensor<128x64xi32> into tensor<8192xi32>
      %expanded_91 = tensor.expand_shape %collapsed_90 [[0, 1]] : tensor<8192xi32> into tensor<8192x1xi32>
      %collapsed_92 = tensor.collapse_shape %broadcasted_83 [[0, 1]] : tensor<128x64xi1> into tensor<8192xi1>
      // input, indices, mask
      %153 = linalg_ext.gather dimension_map = [0] ranged_data(false) signed_indice(true) ins(%152, %expanded_91, %collapsed_92 : tensor<9223372036854775807xf16>, tensor<8192x1xi32>, tensor<8192xi1>) outs(%expanded_89 : tensor<8192x1xf16>) {
      ^bb0(%arg13: f16, %arg14: f16):
        linalg_ext.yield %arg13 : f16
      } -> tensor<8192x1xf16>
      %154 = builtin.unrealized_conversion_cast %153 : tensor<8192x1xf16> to tensor<128x64xf16>

      // b = tl.load(b_ptrs, mask=offs_k[:, None] < K - k * BLOCK_SIZE_K, other=0.0)
      %155 = tensor.empty() : tensor<64x1xi32>
      %156 = linalg.fill ins(%133 : i32) outs(%155 : tensor<64x1xi32>) -> tensor<64x1xi32>
      %157 = arith.index_cast %133 : i32 to index
      %c0_93 = arith.constant 0 : index
      %158 = arith.maxsi %157, %c0_93 : index
      %c64_94 = arith.constant 64 : index
      %159 = arith.minsi %c64_94, %158 : index
      %160 = tensor.empty(%159) : tensor<?x1xi1>
      %true_95 = arith.constant true
      %161 = linalg.fill ins(%true_95 : i1) outs(%160 : tensor<?x1xi1>) -> tensor<?x1xi1>
      %false_96 = arith.constant false
      %162 = tensor.empty() : tensor<64x1xi1>
      %c0_97 = arith.constant 0 : index
      %dim_98 = tensor.dim %162, %c0_97 : tensor<64x1xi1>
      %c0_99 = arith.constant 0 : index
      %163 = arith.addi %c0_99, %159 : index
      %164 = arith.subi %dim_98, %163 : index
      %c1_100 = arith.constant 1 : index
      %dim_101 = tensor.dim %162, %c1_100 : tensor<64x1xi1>
      %c0_102 = arith.constant 0 : index
      %c1_103 = arith.constant 1 : index
      %165 = arith.addi %c0_102, %c1_103 : index
      %166 = arith.subi %dim_101, %165 : index
      %167 = linalg_ext.pad ins(%161 : tensor<?x1xi1>) outs(%162 : tensor<64x1xi1>) pvalue(%false_96 : i1) low = [%c0_99, %c0_102] high = [%164, %166] {
      ^bb0(%arg13: i1):
        linalg_ext.yield %arg13 : i1
      } -> tensor<64x1xi1>
      %collapsed_104 = tensor.collapse_shape %167 [[0, 1]] : tensor<64x1xi1> into tensor<64xi1>
      %168 = tensor.empty() : tensor<64x64xi1>
      %broadcasted_105 = linalg.broadcast ins(%collapsed_104 : tensor<64xi1>) outs(%168 : tensor<64x64xi1>) dimensions = [1]
      %c0_i32_106 = arith.constant 0 : i32
      %c0_i32_107 = arith.constant 0 : i32
      %169 = tensor.empty() : tensor<64x64xi32>
      %170 = linalg.fill ins(%c0_i32_107 : i32) outs(%169 : tensor<64x64xi32>) -> tensor<64x64xi32>
      %171 = tensor.empty() : tensor<64x64xi32>
      %mapped_108 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%arg12, %170 : tensor<64x64xi32>, tensor<64x64xi32>) outs(%171 : tensor<64x64xi32>)
      %172 = llvm.inttoptr %arg1 : i64 to !llvm.ptr
      %view_memref_109 = aux.view %172 to offset: [0], sizes: [9223372036854775807], strides: [1] : !llvm.ptr to memref<9223372036854775807xf16>
      %173 = bufferization.to_tensor %view_memref_109 restrict writable : memref<9223372036854775807xf16>
      %collapsed_110 = tensor.collapse_shape %3 [[0, 1]] : tensor<64x64xf16> into tensor<4096xf16>
      %expanded_111 = tensor.expand_shape %collapsed_110 [[0, 1]] : tensor<4096xf16> into tensor<4096x1xf16>
      %collapsed_112 = tensor.collapse_shape %mapped_108 [[0, 1]] : tensor<64x64xi32> into tensor<4096xi32>
      %expanded_113 = tensor.expand_shape %collapsed_112 [[0, 1]] : tensor<4096xi32> into tensor<4096x1xi32>
      %collapsed_114 = tensor.collapse_shape %broadcasted_105 [[0, 1]] : tensor<64x64xi1> into tensor<4096xi1>
      %174 = linalg_ext.gather dimension_map = [0] ranged_data(false) signed_indice(true) ins(%173, %expanded_113, %collapsed_114 : tensor<9223372036854775807xf16>, tensor<4096x1xi32>, tensor<4096xi1>) outs(%expanded_111 : tensor<4096x1xf16>) {
      ^bb0(%arg13: f16, %arg14: f16):
        linalg_ext.yield %arg13 : f16
      } -> tensor<4096x1xf16>
      %175 = builtin.unrealized_conversion_cast %174 : tensor<4096x1xf16> to tensor<64x64xf16>

      // tt.dot -> linalg.matmul
      %176 = linalg.matmul {__allow_tf32__} ins(%154, %175 : tensor<128x64xf16>, tensor<64x64xf16>) outs(%arg10 : tensor<128x64xf32>) -> tensor<128x64xf32>

      // 更新layout，%5 = BLOCK_SIZE_K * stride_ak(1)
      %177 = tensor.empty() : tensor<128x64xi32>
      %mapped_115 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%arg11, %5 : tensor<128x64xi32>, tensor<128x64xi32>) outs(%177 : tensor<128x64xi32>)
      %178 = tensor.empty() : tensor<64x64xi32>
      // %56 = BLOCK_SIZE_K * stride_bk(%arg6)
      %mapped_116 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%56, %arg12 : tensor<64x64xi32>, tensor<64x64xi32>) outs(%178 : tensor<64x64xi32>)
      scf.yield %176, %mapped_115, %mapped_116 : tensor<128x64xf32>, tensor<128x64xi32>, tensor<64x64xi32>
    }
    // c = accumulator.to(tl.float16)
    %58 = tensor.empty() : tensor<128x64xf16>
    %mapped_23 = linalg.map { arith.truncf } ins(%57#0 : tensor<128x64xf32>) outs(%58 : tensor<128x64xf16>)

    // offs_cm, offs_cn
    %expanded_24 = tensor.expand_shape %mapped [[0, 1]] : tensor<128xi32> into tensor<128x1xi32>
    %59 = tensor.empty() : tensor<128x1xi32>
    %60 = linalg.fill ins(%arg8 : i32) outs(%59 : tensor<128x1xi32>) -> tensor<128x1xi32>
    %61 = tensor.empty() : tensor<128x1xi32>
    %mapped_25 = linalg.map { arith.muli {overflowFlags = #arith.overflow<none>} } ins(%60, %expanded_24 : tensor<128x1xi32>, tensor<128x1xi32>) outs(%61 : tensor<128x1xi32>)
    %expanded_26 = tensor.expand_shape %mapped_8 [[0, 1]] : tensor<64xi32> into tensor<1x64xi32>
    %collapsed_27 = tensor.collapse_shape %mapped_25 [[0, 1]] : tensor<128x1xi32> into tensor<128xi32>
    %62 = tensor.empty() : tensor<128x64xi32>
    %broadcasted_28 = linalg.broadcast ins(%collapsed_27 : tensor<128xi32>) outs(%62 : tensor<128x64xi32>) dimensions = [1]
    %63 = tensor.empty() : tensor<128x64xi64>
    %64 = linalg.fill ins(%arg2 : i64) outs(%63 : tensor<128x64xi64>) -> tensor<128x64xi64>
    %collapsed_29 = tensor.collapse_shape %expanded_26 [[0, 1]] : tensor<1x64xi32> into tensor<64xi32>
    %65 = tensor.empty() : tensor<128x64xi32>
    %broadcasted_30 = linalg.broadcast ins(%collapsed_29 : tensor<64xi32>) outs(%65 : tensor<128x64xi32>) dimensions = [0]
    %66 = tensor.empty() : tensor<128x64xi32>
    %mapped_31 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%broadcasted_30, %broadcasted_28 : tensor<128x64xi32>, tensor<128x64xi32>) outs(%66 : tensor<128x64xi32>)
    %67 = tensor.empty() : tensor<128x64xi64>
    // c_ptrs = c_ptr + layout_c
    %mapped_32 = linalg.map ins(%64, %mapped_31 : tensor<128x64xi64>, tensor<128x64xi32>) outs(%67 : tensor<128x64xi64>)
      (%in: i64, %in_69: i32) {
        %126 = arith.extsi %in_69 : i32 to i64
        %c2_i64 = arith.constant 2 : i64
        %127 = arith.muli %126, %c2_i64 : i64
        %128 = arith.addi %in, %127 : i64
        linalg.yield %128 : i64
      }

    // c_mask计算
    %68 = tensor.empty() : tensor<128x1xi32>
    %69 = linalg.fill ins(%arg3 : i32) outs(%68 : tensor<128x1xi32>) -> tensor<128x1xi32>
    %70 = arith.index_cast %22 : i32 to index
    %c128 = arith.constant 128 : index
    %71 = arith.addi %c128, %70 : index
    %72 = arith.index_cast %arg3 : i32 to index
    %73 = arith.maxsi %72, %70 : index
    %74 = arith.minsi %71, %73 : index
    %75 = arith.subi %74, %70 : index
    %76 = tensor.empty(%75) : tensor<?x1xi1>
    %true = arith.constant true
    %77 = linalg.fill ins(%true : i1) outs(%76 : tensor<?x1xi1>) -> tensor<?x1xi1>
    %false = arith.constant false
    %78 = tensor.empty() : tensor<128x1xi1>
    %c0 = arith.constant 0 : index
    %dim = tensor.dim %78, %c0 : tensor<128x1xi1>
    %c0_33 = arith.constant 0 : index
    %79 = arith.addi %c0_33, %75 : index
    %80 = arith.subi %dim, %79 : index
    %c1 = arith.constant 1 : index
    %dim_34 = tensor.dim %78, %c1 : tensor<128x1xi1>
    %c0_35 = arith.constant 0 : index
    %c1_36 = arith.constant 1 : index
    %81 = arith.addi %c0_35, %c1_36 : index
    %82 = arith.subi %dim_34, %81 : index
    %83 = linalg_ext.pad ins(%77 : tensor<?x1xi1>) outs(%78 : tensor<128x1xi1>) pvalue(%false : i1) low = [%c0_33, %c0_35] high = [%80, %82] {
    ^bb0(%arg9: i1):
      linalg_ext.yield %arg9 : i1
    } -> tensor<128x1xi1>
    %84 = tensor.empty() : tensor<1x64xi32>
    %85 = linalg.fill ins(%arg4 : i32) outs(%84 : tensor<1x64xi32>) -> tensor<1x64xi32>
    %86 = arith.index_cast %31 : i32 to index
    %c64 = arith.constant 64 : index
    %87 = arith.addi %c64, %86 : index
    %88 = arith.index_cast %arg4 : i32 to index
    %89 = arith.maxsi %88, %86 : index
    %90 = arith.minsi %87, %89 : index
    %91 = arith.subi %90, %86 : index
    %92 = tensor.empty(%91) : tensor<1x?xi1>
    %true_37 = arith.constant true
    %93 = linalg.fill ins(%true_37 : i1) outs(%92 : tensor<1x?xi1>) -> tensor<1x?xi1>
    %false_38 = arith.constant false
    %94 = tensor.empty() : tensor<1x64xi1>
    %c0_39 = arith.constant 0 : index
    %dim_40 = tensor.dim %94, %c0_39 : tensor<1x64xi1>
    %c0_41 = arith.constant 0 : index
    %c1_42 = arith.constant 1 : index
    %95 = arith.addi %c0_41, %c1_42 : index
    %96 = arith.subi %dim_40, %95 : index
    %c1_43 = arith.constant 1 : index
    %dim_44 = tensor.dim %94, %c1_43 : tensor<1x64xi1>
    %c0_45 = arith.constant 0 : index
    %97 = arith.addi %c0_45, %91 : index
    %98 = arith.subi %dim_44, %97 : index
    %99 = linalg_ext.pad ins(%93 : tensor<1x?xi1>) outs(%94 : tensor<1x64xi1>) pvalue(%false_38 : i1) low = [%c0_41, %c0_45] high = [%96, %98] {
    ^bb0(%arg9: i1):
      linalg_ext.yield %arg9 : i1
    } -> tensor<1x64xi1>
    %collapsed_46 = tensor.collapse_shape %83 [[0, 1]] : tensor<128x1xi1> into tensor<128xi1>
    %100 = tensor.empty() : tensor<128x64xi1>
    %broadcasted_47 = linalg.broadcast ins(%collapsed_46 : tensor<128xi1>) outs(%100 : tensor<128x64xi1>) dimensions = [1]
    %collapsed_48 = tensor.collapse_shape %99 [[0, 1]] : tensor<1x64xi1> into tensor<64xi1>
    %101 = tensor.empty() : tensor<128x64xi1>
    %broadcasted_49 = linalg.broadcast ins(%collapsed_48 : tensor<64xi1>) outs(%101 : tensor<128x64xi1>) dimensions = [0]
    %102 = tensor.empty() : tensor<128x64xi1>
    %mapped_50 = linalg.map { arith.andi } ins(%broadcasted_47, %broadcasted_49 : tensor<128x64xi1>, tensor<128x64xi1>) outs(%102 : tensor<128x64xi1>)
    %103 = arith.index_cast %22 : i32 to index
    %c128_51 = arith.constant 128 : index
    %104 = arith.addi %c128_51, %103 : index
    %105 = arith.index_cast %arg3 : i32 to index
    %106 = arith.maxsi %105, %103 : index
    %107 = arith.minsi %104, %106 : index
    %108 = arith.subi %107, %103 : index
    %109 = arith.index_cast %31 : i32 to index
    %c64_52 = arith.constant 64 : index
    %110 = arith.addi %c64_52, %109 : index
    %111 = arith.index_cast %arg4 : i32 to index
    %112 = arith.maxsi %111, %109 : index
    %113 = arith.minsi %110, %112 : index
    %114 = arith.subi %113, %109 : index
    %c128_53 = arith.constant 128 : index
    %115 = arith.minsi %108, %c128_53 : index
    %c0_54 = arith.constant 0 : index
    %116 = arith.maxsi %115, %c0_54 : index
    %c64_55 = arith.constant 64 : index
    %117 = arith.minsi %c64_55, %114 : index
    %c0_56 = arith.constant 0 : index
    %118 = arith.maxsi %117, %c0_56 : index
    %c0_i32_57 = arith.constant 0 : i32
    %c0_i32_58 = arith.constant 0 : i32
    %119 = tensor.empty() : tensor<128x64xi32>
    %120 = linalg.fill ins(%c0_i32_58 : i32) outs(%119 : tensor<128x64xi32>) -> tensor<128x64xi32>
    %121 = tensor.empty() : tensor<128x64xi32>
    %mapped_59 = linalg.map { arith.addi {overflowFlags = #arith.overflow<none>} } ins(%mapped_31, %120 : tensor<128x64xi32>, tensor<128x64xi32>) outs(%121 : tensor<128x64xi32>)
    %c0_60 = arith.constant 0 : index
    %c1_61 = arith.constant 1 : index
    %c0_62 = arith.constant 0 : index
    %c0_63 = arith.constant 0 : index
    %extracted = tensor.extract %mapped_59[%c0_62, %c0_63] : tensor<128x64xi32>
    %extracted_64 = tensor.extract %mapped_59[%c1_61, %c0_63] : tensor<128x64xi32>
    %122 = arith.subi %extracted_64, %extracted : i32
    %123 = arith.index_cast %122 : i32 to index
    %c1_65 = arith.constant 1 : index
    %c0_66 = arith.constant 0 : index
    %c0_67 = arith.constant 0 : index
    %extracted_68 = tensor.extract %mapped_59[%c0_66, %c0_67] : tensor<128x64xi32>
    %124 = arith.index_cast %extracted_68 : i32 to index

    // tl.store
    %125 = llvm.inttoptr %arg2 : i64 to !llvm.ptr
    %view_memref = aux.view %125 to offset: [%124], sizes: [%116, %118], strides: [%123, 1] : !llvm.ptr to memref<?x?xf16, #map>
    %extracted_slice = tensor.extract_slice %mapped_23[0, 0] [%116, %118] [1, 1] : tensor<128x64xf16> to tensor<?x?xf16>
    bufferization.materialize_in_destination %extracted_slice in writable %view_memref : (tensor<?x?xf16>, memref<?x?xf16, #map>) -> ()
    return
  }
}

Dialect

triton-linalg 中新增的自定义 dialect 最重要的是 Auxiliar 和 LinalgExt，也为新增 dialect 提供了一个很好的范本：

自定义op
为op实现TilingInterface
为dialect挂DialectInlinerInterface
…

让我们带着 “新引入的dialect是为了cover哪些算子的转换，有什么好处？” 的疑问去阅读一下相关源码。

TableGen 是 LLVM 中用来添加内容(op、dialect、interface、pass等)的一种文件格式，方便，主要是起对象声明等作用。为了方便对相关内容的理解，这里简单介绍一下 TableGen 文件，一些基础语法的概念见： LLVM TableGen 一文。我们以 aux::ViewOp 为例，简单过一下

aux.view在AuxiliaryOps.td中的定义

ViewOp 继承自 Aux_Op 的基类，并注册了多个 interface，使用 DeclareOpInterfaceMethods 声明的interface时需要被重写覆盖，而其他都是默认继承（采用默认实现）。

  
def ViewOp :
  Aux_Op<"view", [
      DeclareOpInterfaceMethods<OpAsmOpInterface, ["getAsmResultNames"]>,
      AttrSizedOperandSegments,
      OffsetSizeAndStrideOpInterface,
      ViewLikeOpInterface]> {

summary 和 description 中分别是该aux.view 简短描述（一般就一句话）和详细描述（包含各个参数示例等）。这里可以了解到 aux.view 的输入为指针、offset、sizes、strides（警觉，memref layout三件套！），会从指针中获得一个 layout 为输入offset、sizes、strides的 memref。

  
  let summary = "To view a ptr as a memref.";
  let description = [{
    Attach offset, sizes, strides to a llvm pointer.
    Example:
    ```mlir
    aux.view %ptr to
      offset: [0],
      sizes: [%size0, 10],
      strides: [1, %stride1]
    : llvm.ptr<f32> to memref<?x10xf32, strided<[1, ?], offset: 0>>
    ```

    This operation creates a new memref descriptor using the base of the
    ptr and applying the input arguments to the other metadata.
    In other words:
    ```mlir
    %dst = aux.view %src to
      offset: [%offset],
      sizes: [%sizes],
      strides: [%strides]
    ```
    means that `%dst`'s descriptor will be:
    ```mlir
    %dst.base = %src
    %dst.aligned = %src
    %dst.offset = %offset
    %dst.sizes = %sizes
    %dst.strides = %strides
    ```
  }];

arguments 描述拉 aux.view 的输入对象以及类型。 Variadic 表示可变长度（表示当前arg可能有多个），后接类型限制。OptionalAttr 表示可选的属性。

关于 Variadic 引用一篇博客的内容做补充通常，Op是没有可变操作数或者只有一个可变操作数。对于后一种情况，可以通过静态可变操作数的定义很容易的推导出动态可变操作数。但是，如果一个Op有多个可变长度操作数(可选的或可变长度的)，需要用SameVariadicOperandSize或AttrSizedOperandSegments特征来表明所有的可变长度操作数都有与之对应的动态值。

  
  let arguments = (ins
    LLVM_AnyPointer:$ptr,
    Variadic<Index>:$offsets,
    Variadic<Index>:$sizes,
    Variadic<Index>:$strides,
    DenseI64ArrayAttr:$static_offsets,
    DenseI64ArrayAttr:$static_sizes,
    DenseI64ArrayAttr:$static_strides,
    OptionalAttr<StrAttr>:$cache_mode);
  let results = (outs AnyMemRef:$result);

assemblyFormat 指定该操作在打印和解析时的格式。

  
  let assemblyFormat = [{
    $ptr `to` `offset` `` `:`
    custom<DynamicIndexList>($offsets, $static_offsets)
    `` `,` `sizes` `` `:`
    custom<DynamicIndexList>($sizes, $static_sizes)
    `` `,` `strides` `` `:`
    custom<DynamicIndexList>($strides, $static_strides)
    attr-dict `:` type($ptr) `to` type($result)
  }];

builder 声明了 aux.view 有多少种 build 的方法，这些方法就表明了在使用 OpBuilder 的 create 函数创建 aux::ViewOp 应该的输入。在TableGen中定义完后，还需要在 AuxiliaryDialect.cpp 中显示编写对应的 ViewOp::build 函数。

*如果td中没有为 op 声明 builder，那说明op的build方法只有一种，直接使用 arguements中所有作为参数。**

  
  let builders = [
    // Build a ViewOp with mixed static and dynamic entries.
    OpBuilder<(ins "MemRefType":$resultType, "Type":$elementType,
      "Value":$source, "OpFoldResult":$offset, "ArrayRef<OpFoldResult>":$sizes,
      "ArrayRef<OpFoldResult>":$strides,
      "StringAttr": $cacheMode,
      CArg<"ArrayRef<NamedAttribute>", "{}">:$attrs)>,
    // Build a ViewOp with static entries.
    OpBuilder<(ins "MemRefType":$resultType, "Type":$elementType,
      "Value":$source, "int64_t":$offset, "ArrayRef<int64_t>":$sizes,
      "ArrayRef<int64_t>":$strides,
      "StringAttr": $cacheMode,
      CArg<"ArrayRef<NamedAttribute>", "{}">:$attrs)>,
    // Build a ViewOp with dynamic entries.
    OpBuilder<(ins "MemRefType":$resultType, "Type":$elementType,
      "Value":$source, "Value":$offset, "ValueRange":$sizes,
      "ValueRange":$strides,
      "StringAttr": $cacheMode,
      CArg<"ArrayRef<NamedAttribute>", "{}">:$attrs)>,
    // Build a ViewOp with dynamic entries and inferred result type.
    OpBuilder<(ins "Type":$elementType, "Value":$source, "Value":$offset,
      "ValueRange":$sizes, "ValueRange":$strides,
      "StringAttr": $cacheMode,
      CArg<"ArrayRef<NamedAttribute>", "{}">:$attrs)>,
    OpBuilder<(ins "Type":$elementType, "Value":$source, "OpFoldResult":$offset,
      "ArrayRef<OpFoldResult>":$sizes,
      "ArrayRef<OpFoldResult>":$strides,
      "StringAttr": $cacheMode,
      CArg<"ArrayRef<NamedAttribute>", "{}">:$attrs)>
  ];
}

extraClassDeclaration 中是以 c++ 代码的形式为 aux.view 注册了一些函数，可以直接使用，这些函数都可以在编译出的 AuxiliaryOps.h.inc 中找到。

  
  let extraClassDeclaration = [{
    /// Returns the dynamic sizes for this subview operation if specified.
    ::mlir::Operation::operand_range getDynamicSizes() { return getSizes(); }

    /// Return the list of Range (i.e. offset, size, stride). Each
    /// Range entry contains either the dynamic value or a ConstantIndexOp
    /// constructed with `b` at location `loc`.
    ::mlir::SmallVector<::mlir::Range, 8> getOrCreateRanges(
        ::mlir::OpBuilder &b, ::mlir::Location loc) {
      return ::mlir::getOrCreateRanges(*this, b, loc);
    }

    // The result of the op is always a ranked memref.
    MemRefType getType() { return getResult().getType().cast<MemRefType>(); }
    Value getViewSource() { return getPtr(); }
    Value getOffset() {
      return getOffsets().empty() ? nullptr : getOffsets()[0];
    }

    /// Return the expected rank of each of the`static_offsets`, `static_sizes`
    /// and `static_strides` attributes.
    std::array<unsigned, 3> getArrayAttrMaxRanks() {
      unsigned resultRank = getResult().getType().cast<ShapedType>().getRank();
      return {1, resultRank, resultRank};
    }

    /// Return the number of leading operands before the `offsets`, `sizes` and
    /// and `strides` operands.
    static unsigned getOffsetSizeAndStrideStartOperandIndex() { return 1; }
  }];

hasVerifier 属性用于控制op是否注册 verify 函数（用于检测构造的行为是否正确），这里表示 aux.view 将会自定义 verify 函数，位于 lib/Dialect/Auxiliary/IR/AuxiliaryDialect.cpp

  
  let hasVerifier = 1;

Auxiliar

Auxiliary Dialect的相关代码位于：

include/triton-linalg/Dialect/Auxiliary
lib/Dialect/Auxiliary

aux.store

看描述有些像 copy 的行为，下面的ir表示将 %c1 存到 %0。

aux.store %c1, %0: tensor<1xf32> to tensor<1xf32>

构造 aux.store 时只需要简单地给定src和dst：

  
Value to, from;
rewriter.create<aux::StoreResourceOp>(op.getLoc(), to, from);

当前在 triton-linalg 中的使用只有 某种情况下 的 tt.store下降，这种情况下 tt.store 下降成了 llvm.inttoptr + aux.view + bufferization.to_tensor + linalg_ext.scatter，我们在后续 Conversion 中将再分析相关的 pattern。

aux.view

在前文简要介绍 TableGen 时已经讲解了 view op 相关的定义，这里不再赘述。aux.view 用于从地址 ptr 中根据 offset & sizes & shapes 获得一个具体的 memref。

当前在 triton-linalg 中的使用是对 ttir 中对指针进行处理，下降为： llvm.inttoptr + aux.view + bufferization.to_tensor，方便后续tensor上的操作。

%ptr = llvm.inttoptr %arg0 : i64 to !llvm.ptr
%view_memref = aux.view %ptr to offset: [0], sizes: [9223372036854775807], strides: [1] : !llvm.ptr to memref<9223372036854775807xf16>
%view_tensor = bufferization.to_tensor %view_memref restrict writable : memref<9223372036854775807xf16>

指针相关的处理逻辑主要在，结合 op conversion 过程理解更好，所以后文遇见再讲。

include/triton-linalg/Dialect/Triton/Utils/PointerMetaInfoTracker.h
lib/Dialect/Triton/Utils/PointerMetaInfoTracker.cpp

aux.optimization_barrier

作为一种表达不要优化的 compiler hint 的 op 存在，例如保护一个空循环不要被消除

scf.for %i = 0 to 128 step %c1 {
  aux.optimization_barrier
}

当前在 triton-linalg 中并没有构造使用，或许是某个 pattern 会构造出特殊的 ir 供之后的 pattern 使用，使用 aux.optimization_barrier 保护这段 ir 不被删除。

aux.print / aux.scalar.print

继承了 DestinationStyleOpInterface，承接 tt.print 的下降。

// triton-linalg-opt  test/Conversion/triton-to-linalg.mlir --convert-triton-to-linalg --split-input-file
%1 = tt.get_program_id x : i32
%2 = tt.get_program_id y : i32
%3 = tt.get_program_id z : i32
aux.scalar.print(%1 : i32) {format = "pid ("}
aux.scalar.print(%2 : i32) {format = ", "}
aux.scalar.print(%3 : i32) {format = ", "}
aux.scalar.print {format = ") "}
%4 = aux.print(%arg0 : tensor<16xi32>) {format = ""} -> (tensor<16xi32>)

为 aux.print 注册了 TilingInterface，根据相关代码：

include/triton-linalg/Dialect/Auxiliary/Transforms/AuxOpTilingInterface.h
lib/Dialect/Auxiliary/Transforms/AuxOpTilingInterface.cpp

可以了解到为一个自定义的op定义它的 TilingInterface 需要重新实现以下函数，感兴趣的同学可以深入学习。

getDestinationOperands
getLoopIteratorTypes
getIterationDomain
getTiledImplementation
getResultTilePosition
generateResultTileValue
generateScalarImplementation

LinalgExt

LinalgExt Dialect的相关代码位于：

include/triton-linalg/Dialect/LinalgExt
lib/Dialect/LinalgExt

LinalgExt 新定义了挺多 op，这里只大概介绍当前在 triton-linalg 中有使用到的op。

linalg_ext.make_rang

根据 input 建立一个 1D 的 static shape tensor，例如以下ir。

%c0_i32 = arith.constant 0 : i32
%c128_i32 = arith.constant 128 : i32
%range = linalg_ext.make_range {operandSegmentSizes = array<i32: 2, 1>} ins(%c0_i32, %c128_i32 : i32, i32) outs(%21 : tensor<128xi32>) -> tensor<128xi32>

用来承接 tt.make_range 的下降。

  
triton language: tl.arange(0, BLOCK_SIZE_M)
ttir: %range = tt.make_range {end = 128 : i32, start = 0 : i32} : tensor<128xi32>
linalg: %range = linalg_ext.make_range {operandSegmentSizes = array<i32: 2, 1>} ins(%c0_i32, %c128_i32 : i32, i32) outs(%21 : tensor<128xi32>) -> tensor<128xi32>

linalg_ext.gather

gather 是一种将非连续内存位置的数据收集到连续内存位置的操作。linalg_ext.gather 的输入一般为 2个(input, indices) 或 3个(input, indices, mask)。

LinalgExtOps.td 中描述到这些operand相互关系关系为

  
- input has shape [i0, i1, ..., in-1]
- indices has shape [Batch0, Batch1, ..., Batchm-1, k]
  - 一共有 [Batch0, Batch1, ..., Batchm-1] 组 indice
  - 每组 indice 有 k 个数： [idx0, idx1, ..., dixk]，所以 k 一定不能为 dynamic
- mask has shape [Batch0, Batch1, ..., Batchm-1]

- init
  - shape [Batch0, Batch1, ..., Batchm-1, o0, o1, ..., on-1].
  - rank >= 2
  - mask 和 init 的 `前 indices.getRanke() - 1`(又称batchNum) 个 dimSize 相同
  - init[idx + batchNum] <= inputType[idx]
  - init 是从 input 中提取出 [Batch0, Batch1, ..., Batchm-1] 组 形状为 [o0, o1, ..., on-1] 的数据

计算行为：

  
for (i0 = 0; i0 < Batch0; ++i0) {
  ...
  for (im-1 = 0; im-1 < Batchm-1; ++im-1) { // [Batch0, Batch1, ..., Batchm-1] 组
    indice = indices[i0, ..., im-1]; // 每组 indice 数据为 k 个数，即 [idx0, idx1, ..., dixk]
    if (mask[i0, ..., im-1]) { // 判断该组是否需要被 mask
      // if region is empty, only copy will apply on init.
      computation(input[indice], init[i0, ..., im-1]);
    }
  }
}

此时，linalg_ext.gather 还有一个 dimension_map 参数，我理解这是给 indice 做 transpose 的。即给长度为 k 的数组 [idx0, idx1, …, dixk]做 permutation(或者说是索引)。所以 dimension_map 存在约束 dimension_map.size() = k，需要包含真实使用的 realIndice 相对 indice 的排布。后续在 computation(input[indice], init[i0, ..., im-1]) 的计算过程，用的就是该 realIndice。

  
SmallVector<int64_t> realIndice(n);
for (int i = 0; i < dimension_map.size(); ++i) {
  realIndice[dimension_map[i]] = indice[i];
}
// 例如 dimension_map = [1, 0], indice = [4, 2]，计算得到 realIndice = [2, 4]

其实在 Triton-Linalg 项目中 build linalg_ext.gather 时，直接给定了 dimension_map = [0]，也就是说这个参数相当于不起作用，没有对 indice 进行 transpose。

linalg_ext.gather 算子可以看作 hlo.gather 的子集，linalg_ext.gather 的 dimension_map 属性可以对应到 hlo.gather 中的 start_index_map 属性。这个属性是用来索引 indice。

算子表示如下，下面的ir可以解释：有4组 indice，每组 indice 有1个数，每组 indice 用于 input(16x8) 中取出大小为 2x4 的数据块，组成输出 4x2x4。

%input: tensor<16x8xf32>
%indices: tensor<4x1xi32>
%mask: tensor<4xi1>
%init: tensor<4x2x4xf32>
%gather = linalg_ext.gather
            dimension_map = [1] // dimension_map定义了如何映射索引和维度
            ranged_data(true) signed_indice(false)
            ins(%input, %indices, %mask: tensor<16x8xf32>, tensor<4x1xi32>, tensor<4xi1>)
            outs(%init: tensor<4x2x4xf32>) {
              // %arg0 代表 %init, %arg1 代表 %input
              ^bb0(%arg0 :f32, %arg1: f32):
                linalg_ext.yield %arg0 : f32
            } -> tensor<4x2x4xf32>

以 op conversion 中 TritonScatteredLoadOpConversion 为例分析，input, indices, mask 都是根据 tt.load 的operand计算得到。

%load = tt.load %ptr, %mask, %other
                  │     │      │
           ┌──────┘     │      └──────┐
           │            │             │
%gather:   ▼            ▼             ▼
       %input         %mask         %init
       %indice

linalg_ext.scatter

scatter 是一种将连续内存位置的数据分散到非连续内存位置的操作。其 operand 与 linalg_ext.gather 相似，gather和scatter可以看作是语义相反的两个操作，linalg_ext.scatter 的输入一般为 2个(update, indices) 或 3个(update, indices, mask)。

LinalgExtOps.td 中描述到这些operand的shape关系为

  
- update
  - shape [Batch0, Batch1, ..., Batchm-1, window0, ..., windown-1]
  - rank >= 2
  - update 可以看成 [Batch0, Batch1, ..., Batchm-1] 组数据，每组数据 [window0, ..., windown-1]
- indice has shape [Batch0, Batch1, ..., Batchm-1, k]
- mask has shape [Batch0, Batch1, ..., Batchm-1].

- init
  - shape [i0, i1, ..., in-1]
  - rank >= 1
  - update[idx + batchNum] <= init[idx]

- dimension_map.size() = indice.back() = k, k不能为dynamic

计算行为：

  
    for (i0 = 0; i0 < Batch0; ++i0) {
      ...
      for (im-1 = 0; im-1 < Batchm-1; ++im-1) {
        indice = wholeIdx[i0, ..., im-1];
        if (mask[i0, ..., im-1]) {
          computation(init[indice], update[i0, ..., im-1]);
        }
      }
    }

算子表示，具体不再赘述，根据 gather 一起理解

%update: tensor<4x2x4xf32>
%indices: tensor<4x1xi32>
%mask: tensor<4xi1>
%init: tensor<16x8xf32>
%scatter = linalg_ext.scatter
            dimension_map = [1]
            ranged_data(true)
            overlap_window(false) signed_indice(true)
            ins(%update, %indice, %mask: tensor<4x2x4xf32>, tensor<4x1xi32>, tensor<4xi1>)
            outs(%init: tensor<16x8xf32>) {
              // %arg0 代表 %update, %arg1 代表 %init
              ^bb0(%arg0 :f32, %arg1: f32):
                linalg_ext.yield %arg0 : f32
            } -> tensor<16x8xf32>

以 op conversion 中 TritonScatteredStoreOpConversion 为例分析，input, indices, mask 都是根据 tt.store 的operand计算得到。

%store = tt.store %ptr, %value, %mask
                    │      │      │
             ┌──────┘      │      └──────┐
             │             │             │
%scatter:    ▼             ▼             ▼
          %indice       %update        %mask
%init: tensor.emnpty

linalg_ext.atomic_rmw \ linalg_ext.gather_atomic_rmw

AtomicRMW 是一种原子读-修改-写（Read-Modify-Write）操作，用于在多线程或并行计算环境中对共享内存进行原子操作。这种操作确保了在对某个内存位置进行读取、修改和写入的过程中，不会被其他线程或进程打断，从而避免数据竞争和不一致性。（来自chatgpt的解释）

triton 中的 atomic类op 除了 atomic_cas，其他都下降成 tt.atomic_rmw

linalg_ext.atomic_rmw 的inputs有一个，inits有两个(src和dst)；linalg_ext.gather_atomic_rmw 的inputs有多个(input, indice, mask)，inits有两个(src和dst)。承接 tt.atomic_rmw 的下降，如果分析出 ptr 的访问行为是连续的就用 linalg_ext.atomic_rmw，反之则用 linalg_ext.gather_atomic_rmw。

linalg_ext.atomic_rmw addf release ins(%input : tensor<4xf32>) outs(%src, %dst : tensor<4xf32>, tensor<4xf32>) -> tensor<4xf32>, tensor<4xf32>

linalg_ext.gather_atomic_rmw addf relaxed ins(%input, %indice, %mask : tensor<4x1xf32>, tensor<4x1xi32>, tensor<4xi8>) outs(%src, %dst : tensor<?xf32>, tensor<4x1xf32>) -> tensor<?xf32>, tensor<4x1xf32>

linalg_ext.atomic_cas / linalg_ext.gather_atomic_cas

AtomicCAS 是原子比较并交换（Compare-And-Swap）的缩写，它是一种常见的原子操作，用于在并发编程中实现线程安全的更新操作。AtomicCAS 操作将内存位置的当前值与预期值进行比较，如果相等，则将该内存位置更新为新值，反之则用原值。（来自chatgpt的解释）

linalg_ext.atomic_cas 的inputs有三个(input, cmp, val)，inits有一个；linalg_ext.gather_atomic_cas 的inputs有四个(input, cmp, val, indice)。承接 tt.atomic_cas 的下降，如果分析出 ptr 的访问行为是连续的就用 linalg_ext.atomic_cas，反之则用 linalg_ext.gather_atomic_cas。

linalg_ext.atomic_cas relaxed ins(%input, %cmp, %val : tensor<128xi32>, tensor<128xi32>, tensor<128xi32>) outs(%init : tensor<128xi32>) -> tensor<128xi32>

linalg_ext.gather_atomic_cas release ins(%input, %cmp, %val, %indice: tensor<?xi32>, tensor<128xi32>, tensor<128xi32>, tensor<128xi64>) outs(%init : tensor<128xi32>) -> tensor<128xi32>

linalg_ext.pad

pad行为，构造时需要 ins, outs, pvalue(pad用的value), low(下界), high(上届)。

%pad = linalg_ext.pad
  ins(%input:tensor<4x4xf32>)
  outs(%init:tensor<6x8xf32>)
  pvalue(0.0:f32)
  low = [1, 2]
  high = [1, 2] {} -> tensor<6x8xf32>

一般用作将 dynamic shape 给 pad 成 static shape，在 triton-linalg 中用来表示可变 mask 的信息，例如 offs_k[None, :] < K - k * BLOCK_SIZE_K，会构造类似下面的ir

%71 = arith.muli %arg9, %c64_i32 : i32
%72 = arith.subi %arg5, %71 : i32

// mask，当k满足%72>0时，为true；反之为false
%73 = arith.index_cast %72 : i32 to index
%74 = arith.maxsi %73, %c0 : index
%75 = arith.minsi %74, %c64 : index
// 保证块大小 小于BLOCK_SIZE_K
%76 = tensor.empty(%75) : tensor<1x?xi1>
%77 = linalg.fill ins(%true : i1) outs(%76 : tensor<1x?xi1>) -> tensor<1x?xi1>
%78 = arith.subi %c64, %75 : index
%79 = linalg_ext.pad ins(%77 : tensor<1x?xi1>) outs(%39 : tensor<1x64xi1>) pvalue(%false : i1) low = [0, 0] high = [0, %78] {
^bb0(%arg13: i1):
  linalg_ext.yield %arg13 : i1
} -> tensor<1x64xi1>

linalg_ext.scan

scan 操作，也称为前缀和（prefix sum），是一种常见的并行算法，用于处理数组或序列。scan 操作对输入序列的每个元素应用某种二元操作（如加法或乘法），并产生一个新的序列，其中每个元素是输入序列中所有前面元素的累积结果。（来自chatgpt的解释）

以加法为例：

  
B[0] = A[0]
B[1] = A[0] + A[1]
B[2] = A[0] + A[1] + A[2]
B[3] = A[0] + A[1] + A[2] + A[3]
B[4] = A[0] + A[1] + A[2] + A[3] + A[4]

该算子的形式如下，沿着给定的 dimensions 对 input 执行 scan 算法。用于承接 tt.scan 的下降。

%scanned = linalg_ext.scan
    ins(%input:tensor<16x32x64xf32>)
    outs(%output, %init: tensor<16x32x64xf32>, tensor<16x64xf32>)
    dimension = [1]
    {
    ^bb0(%in: f32, %out: f32, %init: f32):
      %0 = arith.addf %init, %in: f32
      linalg_ext.yield %0, %0: f32, f32
    }

linalg_ext.libdevice_call / linalg_ext.scalar_libdevice_call`

承接 tt.extern_elementwise 的下降，若返回值为标量，则下降成 linalg_ext.scalar_libdevice_call；若返回值为张量，则下降成 linalg_ext.libdevice_call。

%libdevicecall = linalg_ext.libdevice_call
    ins(%arg1, %arg2 : tensor<16x32x64xf32>, tensor<16x32x64xf32>)
    outs(%init: tensor<16x32x64xf32>)
    symbol = "__cn_vector_add_f32_rn" -> tensor<16x32x64xf32>

%libdevicecall = linalg_ext.scalar_libdevice_call
    ins(%arg0 : f32)
    symbol = "__cn_scalar_abs_f32" -> f32

linalg_ext.assert

assert op是用来 debug 的，linalg_ext.assert 输入为一个 condition tensor，一个 message string，如果 condition 是 false 的话（应该是 condition tensor 中的每个值都满足），就会打印 message 并中断程序，和c++中的 assert(condition && "messagge info") 效果一样。用来承接 tt.assert下降。

%1 = linalg_ext.assert {msg = "x > 0"} ins(%arg0 : tensor<32xi32>) -> tensor<32xi32>

Analysis

Analysis 起到了指导 pass 优化、ir 下降等作用。Triton-Linalg 仓库中的 Analysis 文件大抵是指 AxisInfoAnalysis。

但本文想把 ptr 分析中使用的 Analysis 放在该节。主要有 AxisInfo 、 mask 、 PointerInfo 三部分。

ptr

在 load / store / atomic 算子的下降过程中，会用到 ptr，需要对指针进行分析以获得真实的目标 memref。最终表现为 llvm.int_to_ptr + aux.view，而地址偏移和 mask 等信息表现为后序ir实际读写的memref大小。

PtrInfo 类包含了以下信息。

PtrInfo 类主要在 load / store / atomic 的下降中使用，可以先看下文中的 Conversion 节，再返回来看此处。

  
struct PtrInfo {
  Value memref;
  SmallVector<OpFoldResult> offsets;
  SmallVector<OpFoldResult> sizes;
  SmallVector<DimInfo> dimInfos;
  SmallVector<int64_t> permutations;
  bool isMaskTrackerFailed = false;
};

这里的 DimInfo 描述了最内维(最低维)的行为。有三种模式，contiguous、 broadcast以及other。

contiguous 表示最低维的数据是连续的，例如1234..k1234..k1234..k1234..k，那么这里 contigSize 就是 k

这对应着 tl.max_contiguous max_contiguous(input, values)：对于每个维度i，标识input[i]中每values[i]个相邻元素是连续的例如 values = [4], 则 input 可以是 [0, 1, 2, 3, 8, 9, 10, 11]

broadcast 表示最低维的数据是broadcast的行为的，例如1111222233334444...kkkk，这里的 broadcastSize 就是 4

这对应着 tl.max_constany max_constany(input, values)：对于每个维度i，标识input[i]中每values[i]个相邻元素是常数例如 values = [4], 则 input 可以是 [0, 0, 0, 0, 1, 1, 1, 1]

使用 tl.max_contiguous & tl.multiple_of 是为了标识加载时数据的连续性，这样编译器就不会离散得处理这些数据，而是连续得去处理。

  
offs_am = (pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M
->
offs_am = tl.max_contiguous(tl.multiple_of((pid_m * BLOCK_SIZE_M + tl.arange(0, BLOCK_SIZE_M)) % M, BLOCK_SIZE_M), BLOCK_SIZE_M)

tl.multiple_of(input, values)：对于每个维度i，标识input[i]中所有元素都是 values[i] 的倍数例如 values = [2], 则 input 可以是 [0, 2, 4, 6, 8]

分析 ptr 信息的相关代码主要在 TritonPtrContiguousConversionBase::getPtrInfo 函数中，会去分别利用：

AxisInfoLattice (include/triton-linalg/Analysis/AxisInfoAnalysis.h) ：获得数据的特征，连续性这些
MaskTracker (include/triton-linalg/Dialect/Triton/Utils/MaskTracker.h) ：收集 mask 信息
PointerMetaInfoTracker(include/triton-linalg/Dialect/Triton/Utils/PointerMetaInfoTracker.h) ：计算真实的地址(原始地址+偏移)

以获得 PtrInfo 中的各类信息。最后这些信息组成了具体处理的memref的 offsets, sizes, strides，以及可能的 permutation。

这部分内容太多了，大家感兴趣欢迎具体阅读源码。下文只是简单介绍下，传统功夫，点到为止。

AxisInfo

include/triton-linalh/Analysis/AxisInfoAnalysis.h
lib/Analysis/AxisInfoAnalysis.cpp
include/triton-linalg/Dialect/Triton/Interfaces/InferAxisInfoInterface.h
lib/Dialect/Triton/Interfaces/InferAxisInfoInterface.cpp

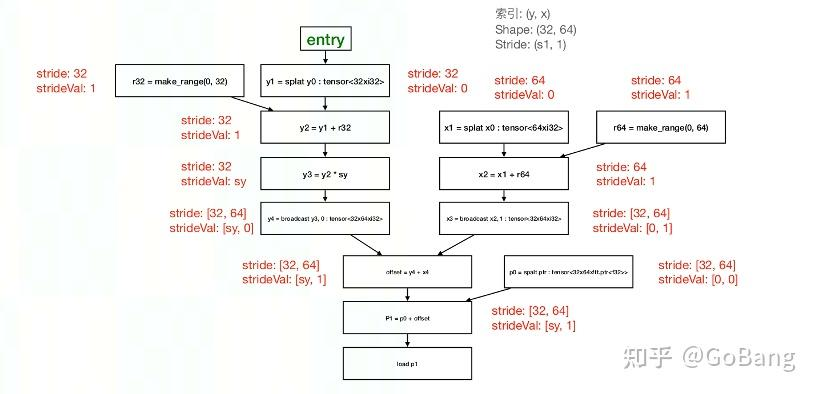
In short: triton 官方的 AxisInfo 会对 load、store 等对指针进行操作的 op 及相关 op 进行跟踪，分析出 divisibility, contiguity, constancy 信息，从而辅助之后的 pass 进行，以获得高 IO 效率。 Triton-Linalg 中的 AxisInfoExt 将 contiguity, constancy 拆成了 stride, strideValue, rank，以适配 SIMD 架构的 DSA 中多维访存指令。

Triton-Linalg 的 AxisInfo 主要使用 AxisInfoExt 类来记录信息。这个类是基于 triton/include/triton/Analysis/AxisInfo.h 修改的。所以理解这部分可以先去看看 triton 官方AxisInfo。

信息说明

divisibility：维度i上，所有元素的最大二次幂公约数。在ttir中经常可以blockArg上有attr： (%arg0: !tt.ptr<f32> {tt.divisibility = 16 : i32}。divisibility这个参数用来计算alignment。
stride: 维度i上，每 stride[i] 个相邻元素是连续的。对应 tl.max_contiguous(input, values) 的 values。
strideValue: 维度i上，两个相邻连续元素的差值为 strideValue[i]。对应着 tl.multiple_of(input, values) 的 values。如果 strideValue = 0 则代表重复元素，如果 strideValue = 1 则代表连续元素。
constantValue：该 lattice 中的 constant value

divisibilty 代表指针指向的地址能被其整除。例如 !tt.ptr<f32> 类型的指针的 divisibilty = 16.
triton 官方的 AxisInfoAnalysis 会记录三个信息: divisbilty, contiguity, constancy，其中 contiguity 和上文的 stride 是一个意思

以下面两种数据为例，上述三种信息的值为：

  
[[10, 11, 12, 13, 18, 19, 20, 21],
 [20, 21, 22, 23, 28, 29, 30, 31]]
- divisibility: [1, 2]
- stride: [4, 2]
- strideValue: [1, 10]

[[12, 16, 20, 24],
 [13, 17, 21, 25],
 [14, 18, 22, 26],
 [15, 19, 23, 27]]
- divisibility: [4, 1]
- stride: [4, 4]
- strideValue: [1, 4]

若要从某个地址上取 tensor<8x32xi32> 的数据，分析出 divisibility = [1, 1], stride = [8, 32], strideValue = [1, 0]，这说明：

shape[0] = 8 & stride[0] = 8 & strideValue[0] = 1 -> 第 0 维上每 8 个数据连续
shape[1] = 32 & stride[1] = 32 & strideValue[1] = 0 -> 第 1 维上的每 32 个数据相同

信息获取

这些信息有两种获得途径，第一种是使用人为 hint 直接挂上，后续从 op 上的 attr 收集；第二种是使用 AxisInfoAnalysis 直接分析。

hint

hint 的方式是人为在写 kernel 时通过 max_contiguous、max_constany、multiple_of 等 hint op 来提示编译器数据的特殊性，以指导编译器的下降行为。人为给定的hint的优先级高于分析出来的。

  
// lib/Dialect/Triton/Interfaces/InferAxisInfoInterface.cpp
if (Attribute attr = op->getAttr("tt.divisibility")) {
  auto vals = attr.cast<DenseElementsAttr>().getValues<int>();
  divisibility = AxisInfoExt::DimVectorT(vals.begin(), vals.end());
}
if (Attribute attr = op->getAttr("tt.contiguity")) {
  auto vals = attr.cast<DenseElementsAttr>().getValues<int>();
  stride = AxisInfoExt::DimVectorT(vals.begin(), vals.end());
  strideValue = AxisInfoExt::DimVectorT(vals.size(), 1); // 连续，所以 strideValue 全 1
}
if (Attribute attr = op->getAttr("tt.constancy")) {
  assert(!op->getAttr("tt.contiguity") &&
         "Get tt.constancy and tt.contiguity attribute at the same op");
  auto vals = attr.cast<DenseElementsAttr>().getValues<int>();
  stride = AxisInfoExt::DimVectorT(vals.begin(), vals.end());
  strideValue = AxisInfoExt::DimVectorT(vals.size(), 0); // 常量，所以 strideValue 全 0
}

分析

采用分析的方式是会构建一个传递的链条，从某个起点(例如tt.make_range)一直追溯到 load / store 操作的 ptr。整个传递算法是基于MLIR官方提供的数据流分析算法，通过定义每个算子的转移函数，进而推导出全图的连续性信息。

传递时，例如传递的时候某个op的producder的contiguity分别等于[64, 1]和[64, 64]，那么合并(求最小公倍数)后也是[64,1]

引自：浅谈寒武纪开源的Triton-Linalg编译器前端

使用 AxisInfo 优化访存行为

分析连续性后，例如存在相同的element，下降成 extract_slice + load + expand_shape + store
当分析不出连续性，至少为带mask的兜底优化：不带mask，都load上来，然后用select %mask %load %other来获得真实值。这个优化在simt中收益或许不大，因为有memory-coalesce

MaskTracker

  
include/triton-linalg/Dialect/Triton/Utils/MaskTracker.h
lib/Dialect/Triton/Utils/MaskTracker.cpp

通过 MaskTracker 来分析 load 和 store 时所使用的mask的信息。

  
MaskTracker maskTracker;
if (mask) {
  maskTracker.parse(mask, loc, rewriter);

在分析 mask 时，将所有情况归纳为 Scalar, SimpleRange, Mask 三类(Result)，以方便后序下降处理。

在 parse 时，会递归地往前遍历，直到收集完能表达 mask 的完整信息。所有遍历到的 parseVal 可以被分成了三类情况处理：

parseVal 的 type 是 IntegerType，即直接是一个标量，来自于 arith 的标量计算
parseVal 的 defineOp 为特定 op 时
parseVal 没有 defineOp 时(说明已经到 blockArg 了)

详细了解请自行阅读 lib/Dialect/Triton/Utils/MaskTracker.cpp，下文只以上述 ir 为例说明 mask parse 的过程。

由于 mask 分析时还没完成 triton-to-linalg 的转换，我们不妨以 ttir 中 tt.load 相关的 mask 计算为例。

triton-lang tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)

// 下面的ir实现 mask=offs_k[None, :] < K - k * BLOCK_SIZE_K
%21 = tt.make_range {end = 64 : i32, start = 0 : i32} : tensor<64xi32> // offs_k = tl.arange(0, BLOCK_SIZE_K)
%29 = tt.expand_dims %21 {axis = 0 : i32} : tensor<64xi32> -> tensor<1x64xi32> // offs_k[None, :]
%66 = arith.muli %arg9, %c64_i32 : i32 // k * BLOCK_SIZE_K， %arg9 是 for 循环的 blcokArg，表示 k
%67 = arith.subi %arg5, %66 : i32 // K - k * BLOCK_SIZE_K， %arg5 表示 K
%68 = tt.splat %67 : i32 -> tensor<1x64xi32>
%69 = arith.cmpi slt, %29, %68 : tensor<1x64xi32> // offs_k[None, :] < K - k * BLOCK_SIZE_K
%70 = tt.broadcast %69 : tensor<1x64xi1> -> tensor<128x64xi1>
// tl.load(a_ptrs, mask=offs_k[None, :] < K - k * BLOCK_SIZE_K, other=0.0)
%71 = tt.load %arg11, %70, %cst : tensor<128x64x!tt.ptr<f16>>

由上面的 ir 中的 mask 可以得到下面的数据流

                               ┌►tt.expand_dims─►tt.make_range
mask─►tt.broadcast─►arith.cmpi─┤
                               └►tt.splat─►arith.subi─►arith.muli

(1) tt.broadcast

继续 parse src (来自 arith.cmpi)

(2) arith.cmpi

继续 parse lhs (来自 tt.expand_dims) 和 rhs (来自 tt.splat)。

parse lhs 拿到 tt.expand_dims 返回的 Result(SimpleRange)
parse rhs 拿到 tt.splat 返回的 Failure，停止。

如果不停止，会进入 compareSimpleRange 将 parse lhs 的 Result(SimpleRange) 和 parse rhs 的 Result(Scalar) 给结合起来，用于计算 mask 的新上届和下届。

(3) tt.expand_dims

继续 parse src (来自 tt.make_range)。

拿到 tt.make_range 返回的 Result(SimpleRange)，继续通过 expandDimRange 跟踪。

  
// axis = 1
self.dims.insert(self.dims.begin() + axis, rewriter.getIndexAttr(1)); // 此时 self.dims = [0, 1]
self.axis += 1; // self.axis = 1

(4) tt.make_range

返回的 Result 为 SimpleRange

  
SimpleRange ret;
ret.start = rewriter.getIndexAttr(start); // rangeOp.getStart()
ret.end = rewriter.getIndexAttr(end); // rangeOp.getEnd()
ret.dims.push_back(rewriter.getIndexAttr(shape[0]));
ret.axis = 0;

(5) tt.splat

继续 parse src(来自 arith.subi)

拿到 arith.subi 返回的 Failure，停止。

如果 parse src 返回的 Result 为 Scalar，那么将 SplatVisitor，主要处理逻辑如下

  
for (auto s : dstShape) // dstShape = [1, 64]
  self.dims.push_back(rewriter.getIndexAttr(s));

(6) arith.subi

继续 parse lhs (来自 blockArg) 和 rhs (来自 arith.muli)。

parse lhs 拿到 blockArg 返回的 Result(Scalar)
parse rhs 拿到 arith.muli 返回的 Failure，结束。

但如果 parse rhs 返回的不是 Failure，那么会进入 BinaryVisitor，将 parse lhs 和 parse rhs 返回的 Result 给使用 lib/Utils/Utils.cpp 中的 subOFRs 结合起来，组成新的 Result。

subOFRs 的主要逻辑就是先尽量 fold 掉一些特殊的 sub 计算，没有 fold 成功的话就把 sub 计算的 lhsType 和 rhstype 都转为 index，再做 sub。

(7) blockArg

由于它的 type 是 IntegerType，即一个 scalarVal，所以进入 parseIntScalar 函数，直接通过 arith.index_cast 转为 index 类型。

  
auto castOp = rewriter.create<arith::IndexCastOp>(
    loc, rewriter.getIndexType(), scalar);
Scalar ret;
ret.scalar = castOp.getResult();

(8) arith.muli

由于 defineOp 不属于下面列表，所以进入 parseUnknownValue 函数。但由于 type 并不是 ShapeType 所以 parse 在这里 failed。

  
return llvm::TypeSwitch<Operation *, FailureOr<Result>>(defOp)
    .Case<arith::ConstantOp, arith::AddIOp, arith::AndIOp, arith::CmpIOp,
          arith::SubIOp, arith::ExtSIOp, arith::TruncIOp,
          triton::MakeRangeOp, triton::BroadcastOp, triton::ExpandDimsOp,
          triton::SplatOp, triton::TransOp>(
        [&](auto op) { return parseOp(op); })
    .Default([&](Operation *) { return parseUnknownValue(operand); });

(9) arith.constant

当 constant 的值来自于单个 denseVal的 splat，即 arith.constant dense : tensor<axbxi32>。

直接从其中抽出最根本的值(用 tensor.extract 或根据 denseVal 的特性取出来)，然后逻辑 parseIntScalar 相似。

  
// value 是从 arith.constant 中提取出来的值
auto op =
    rewriter.create<arith::ConstantIndexOp>(loc, value.getSExtValue());
Scalar ret;
ret.scalar = op.getValue();

PointerMetaInfoTracker

  
include/triton-linalg/Dialect/Triton/Utils/PointerMetaInfoTracker.h
lib/Dialect/Triton/Utils/PointerMetaInfoTracker.cpp

文件中定义了两类 tracker

TensorPointerMetaInfoTracker
- 主要记录 base, sizes, strides, offsets, order 这些信息
- 主要处理对象 tt.make_tensor_ptr, tt.advance
PointerMetaInfoTracker
- 主要记录 base, offset
- 主要处理对象 tt.addptr/tt.bitcast/tt.splat/tt.broadcast/tt.expand_dims

以 PointerMetaInfoTracker 为例，一直 track 到类型为 PointerType 的blockArg。

以下面的ir为例，我们跟踪一下流程：

// a_ptrs = a_ptr + off[None, :]
%range = tt.make_range {end = 64 : i32, start = 0 : i32} : tensor<64xi32>
%expand = tt.expand_dims %range {axis = 0 : i32} : tensor<64xi32> -> tensor<1x64xi32>
%broadcast = tt.broadcast %expand : tensor<1x64xi32> -> tensor<128x64xi32>
// 把 a_ptr splat 成 对应 shape
%splat = tt.splat %arg0 : !tt.ptr<f16> -> tensor<128x64x!tt.ptr<f16>>
%addptr = tt.addptr %splat, %broadcast : tensor<128x64x!tt.ptr<f16>>, tensor<128x64xi32>

在 %arg0 处会第一次创建 arith.constant 0 : i32 作为 offset，然后一直反向传回去。会为 offset 一直创建 op。

            ┌►tt.splat────►%arg0 (a_ptr)
            │
tt.addptr--►│
            │
            └►tt.broadcast─►tt.expand_dims

Conversion

include/triton-linalg/Conversion
lib/Conversion

triton-linalg 的 Conversion 部分包含了以下四种 Dialect-to-Dialect 的 Conversion，覆盖了 ttir 中可能出现的ir。

ArithToLinalg
MathToLinalg
TritonToLinalg
TritonToTensor(目前只有 tt.cat 到 tensor.insert_slice 的转换，本质上也是 tt.ops 的下降，所以就放在 TritonToLinalg 一起讲)

arith.ops / math.ops

这两个 Conversion 都是为了将 输出为 tensor 的 arith.ops / math.ops 转化为 linalg.map{arith.ops} / linalg.map{math.ops}，以方便后续对 linalg-on-tensor 的 ir 表示统一处理（例如 tile 和 bufferize）。当输出为标量时不处理。

(1) arith.constant

完成以下转换：

arith.constant dense<0.0> : tensor<axf32>
->
%cst = arith.constant 0.0 : f32
%empty = tensor.empty() : tensor<axf32>
%fill = linalg.fill ins(%cst : f32) outs(%empty : tensor<axf32>) -> tensor<axf32>

当 arith.constant 的值都是一样 ArithConstantPattern 才会成功，对于下面的 constant 是不会转为 linalg.fill 的。

%cst_tensor = arith.constant dense<[0, 1, 2, 3]> : tensor<4xi32>

(2) arith.select

完成以下转换：

cond 为 tensor 时，直接作为 linalg.map 的 ins

%select = arith.select %cond, %trueVal, %falseVal : tensor<128xf32>
->
%empty = tensor.empty() : tensor<128xf32>
%mapped = linalg.map { arith.select } ins(%cond, %trueVal, %falseVal : tensor<128xi1>, tensor<128xf32>, tensor<128xf32>) outs(%empty : tensor<128xf32>)

cond 为标量(i1) 时，通过 fill 生成一个表示 cond 的 tensor，使用 fill 作为linalg.map 的 ins

%select = arith.select %cond, %trueVal, %falseVal : tensor<128xf32>
->
%empty = tensor.empty() : tensor<128xi1>
%fill = linalg.fill ins(%cond : i1) outs(%empty : tensor<128xi1>) -> tensor<128xi1>
%empty1 = tensor.empty() : tensor<128xf32>
%mapped = linalg.map { arith.select } ins(%fill, %trueVal, %falseVal : tensor<128xi1>, tensor<128xf32>, tensor<128xf32>) outs(%empty1 : tensor<128xf32>)

其他 arith.ops / math.ops

剩下这些op的都有 SameOperandsAndResultType，因此每个 operand 的 type 完全相同，且这些op只有单个输出。

转换函数逻辑较为简单，获取 resultType 后以 operands 来创建 linalg.map，主要的逻辑在 GenericOpPattern。完成以下转换：

%add = arith.addi %lhs, %rhs : tensor<128xi32>
->
%mapped = linalg.map { arith.addi } ins(%lhs, %rhs : tensor<128xi32>, tensor<128xi32>) outs(%empty : tensor<128xi32>)

load / store / mask

由于 tt.load 和 tt.store 的下降 pattern 比较多，切都依赖于 mask 和 ptr 分析，所以单独拿出来讲。

load / store

在 triton-linalg/lib/Conversion/TritonToLinalg/LoadStoreConversion.cpp 中定义了多种情况下的 conversion pattern，根据 pattern benefit 取分开。高 benefit 的 pattern 下降得到的 ir 理论上有更好的 performance。

benefit = 100
- TritonContiguousLoadOpConversion, TritonContiguousStoreOpConversion
- TritonScalarLoadOpConversion, TritonScalarStoreOpConversion
benefit = 1
- TritonTensorPtrLoadOpConversion, TritonTensorPtrStoreOpConversion
benefit = 0
- TritonScatteredLoadOpConversion, TritonScatteredStoreOpConversion

1.TritonContiguousLoadOpConversion, TritonContiguousStoreOpConversion

首先判断是否是 TensorPointerType。

PointerType 的一些形式：
!tt.ptr
!tt.ptr<tensor<2xf32» 这就是 TensorPointerType， tl.make_block_ptr 最后会转成这个
!tt.ptr<!tt.ptr> PointerType 的 getPointeeType 方法会获得 PointerType 内的类型。上面三个分别获得 f32, tensor<2xf32>, !tt.ptr

然后进入 getPtrInfo 函数从指针中获得相关信息，接下来进入指针信息分析。关于 ptr 和 mask 的分析细节请看接下来的两节。

如果成功分析得到 PtrInfo，对于 load，则使用 bufferization.to_tensor + linalg.copy 直接将综合 mask 和地址偏移信息后的具体数据给copy出来；对于 store，则使用 bufferization.materialize_in_destination 直接将数据拷贝到对应的 memref(从ptr中得到) 上。

TritonTensorPtrLoadOpConversion, TritonTensorPtrStoreOpConversion

load 和 store 的结果为 scalar，直接使用 memref.load 和 memref.store 承接。

TritonScatteredLoadOpConversion, TritonScatteredStoreOpConversion

getPtrInfo 分析失败后，无法连续地 load 或 store 数据，使用 linalg_ext.gather 和 linalg_ext.scatter 分别承接 load 和 store 的下降。

linalg_ext.gather 和 linalg_ext.scatter 在上文都已经说过了，不记得可以回顾下。

atomic ops

triton 中的 atomic类op 除了 atomic_cas，其他都下降成 tt.atomic_rmw

由于 atomic op(tt.atomic_cas 和 tt.atomic_rmw) 也对 ptr 进行操作了，所以也有多种下降pattern，尽量分析出连续的情况。

LinalgExt 中也定义了对应的 op 来承接下降。例如承接 tt.atomic_rmw 的下降，如果分析出 ptr 的访问行为是连续的就用 linalg_ext.atomic_rmw，反之则用 linalg_ext.gather_atomic_rmw。

具体的pattern请自行阅读：

  
lib/Conversion/TritonToLinalg/AtomicRmwConversion.cpp
lib/Conversion/TritonToLinalg/AtomicCASConversion.cpp

AtomicRMW 是一种原子读-修改-写（Read-Modify-Write）操作，用于在多线程或并行计算环境中对共享内存进行原子操作。这种操作确保了在对某个内存位置进行读取、修改和写入的过程中，不会被其他线程或进程打断，从而避免数据竞争和不一致性。

tt.ops

代码中包含了很多 triton.ops 的下降 pattern，除了 atomic 以及 load, store。这节也只介绍除 atomic/load/store 之外的 tt.ops 下降 pattern。

lib/Conversion/TritonToLinalg/TritonToLinalg.cpp

可以注意到，许多pattern的代码都有使用 TypeConverter 修改 ResultType 的行为。

  
auto type = typeConverter->convertType(op.getResult().getType());
if (!type)
  return failure();

这个 TypeConverter 来源于自定义的 TritonLinalgTypeConverter。主要实现：若输入的 Type 是 triton::PointerType 时，这段代码会将其修改为 IntegerType(64)，将指针等同为i64类型（后续直接从该i64表示的地址中取数），即

  
!tt.ptr<f32> -> i64
!tt.ptr<!tt.ptr<f16>> -> i64
# 若 RankedTensorType 的 eleType 为 PointerType，则也会将 PointerType 转为 i64
tensor<256x!tt.ptr<f32>> -> tensor<256xi64>

虽然这样不管 !tt.ptr 中的 elemType 直接转为 i64 导致现在损失了 elemType 信息，但是在 LoadStoreConversion 时会直接使用 tt.load 的 resultType 的 elemType。

tt.func / tt.return / tt.call

直接下降到 FuncDialect 中对应的 func.func, func.return, func.call op。

tt.broadcast

tt.broadcast 会改变 dimSize 为 1 的维度，这和 linalg.broadcast 会同时扩展维度的行为不一致，所以需要先使用 tensor.collapse_shape fold 掉 unitDim，再用 linalg.broadcast 扩展到对应 resultType。

tt.broadcast %arg0 : tensor<1x32x1xf32> -> tensor<2x32x4xf32>
->
%collapsed = tensor.collapse_shape %arg0 [[0, 1, 2]] : tensor<1x32x1xf32> into tensor<32xf32>
%empty = tensor.empty() : tensor<2x32x4xf32>
%broadcasted = linalg.broadcast ins(%collapsed : tensor<32xf32>) outs(%empty : tensor<2x32x4xf32>) dimensions = [0, 2]

tt.splat

tt.splat 一般用来将一个标量数据 splat 到一个 tensor，和 linalg.fill 语义相同。

%splat = tt.splat %arg0 : i32 -> tensor<1024xi32>
->
%empty = tensor.empty() : tensor<1024xi32>
%fill = linalg.fill ins(%arg0: i32) outs(%empty : tensor<1024xi32>) -> tensor<1024xi32>

tt.expand_dims

tt.expand_dims 用来扩展维度，有一个输入来指定需要扩展的维度，一次仅扩展1维，扩展后的维度dimSize为1。

%expand = tt.expand_dims %arg0 {axis = 2: i32} : tensor<8x4xi32> -> tensor<8x4x1xi32>
->
%expand = tensor.expand_shape %arg0 [[0], [1, 2]] : tensor<8x4xi32> into tensor<8x4x2xi32>

tt.addptr

tt.addptr 用来实现指针的加法操作，lhs 为 ptr，rhs 为 offset。operand的shape相同，可以为rankedTensor(下降为linalg.map{addi})或scalar(下降为arith.addi)。offset 可以理解为是数组的下标，以标量相加为例， ptr 是取数的地址， %offset 是取的数个数。

当ptr为标量时：

%scalar_addptr = tt.addptr %arg0, %arg1: !tt.ptr<f16>, i32
->
%0 = arith.extsi %arg1 : i32 to i64
// 相当于取了 %arg1 个类型为 f16 的数据，所以需要乘以2(=16/8)对齐地址
%c2_i64 = arith.constant 2 : i64
%1 = arith.muli %0, %c2_i64 : i64
%2 = arith.addi %arg0, %1 : i64

%tensor_addptr = tt.addptr %arg0, %arg1: tensor<256x!tt.ptr<f32>>, tensor<256xi32>
->
%mapped = linalg.map ins(%arg0, %arg1 : tensor<256xi64>, tensor<256xi32>) outs(%empty : tensor<256xi64>)
  (%in: i64, %in_0: i32) {
    %0 = arith.extsi %in_0 : i32 to i64
    %c4_i64 = arith.constant 4 : i64
    %1 = arith.muli %0, %c4_i64 : i64
    %2 = arith.addi %in, %1 : i64
    linalg.yield %2 : i64
  }

当ptr为rankedTensor时，我们构造以下计算 b_ptrs 的ir，下降得到：

// b_ptrs = b_ptr + (offs_k[:, None] * stride_bk + offs_bn[None, :] * stride_bn)
tt.func @b_ptrs(%b_ptr: !tt.ptr<f16>, %offs_bn: tensor<64xi32>, %stride_bk: i32) {
  %0 = tt.make_range {end = 64 : i32, start = 0 : i32} : tensor<64xi32>
  %1 = tt.expand_dims %0 {axis = 1 : i32} : tensor<64xi32> -> tensor<64x1xi32>
  %2 = tt.splat %stride_bk : i32 -> tensor<64x1xi32>
  %3 = arith.muli %1, %2 : tensor<64x1xi32>
  %4 = tt.expand_dims %offs_bn {axis = 0 : i32} : tensor<64xi32> -> tensor<1x64xi32>
  %5 = tt.broadcast %3 : tensor<64x1xi32> -> tensor<64x64xi32>
  %6 = tt.broadcast %4 : tensor<1x64xi32> -> tensor<64x64xi32>
  %7 = arith.addi %5, %6 : tensor<64x64xi32>
  %8 = tt.splat %b_ptr : !tt.ptr<f16> -> tensor<64x64x!tt.ptr<f16>>
  %9 = tt.addptr %8, %7 : tensor<64x64x!tt.ptr<f16>>, tensor<64x64xi32>
  tt.return
}
->
其中 `tt.addptr` 下降得到的部分ir是
%9 = linalg.fill ins(%arg0 : i64) outs(%8 : tensor<64x64xi64>) -> tensor<64x64xi64>
%10 = tensor.empty() : tensor<64x64xi64>
%mapped_4 = linalg.map ins(%9, %mapped_3 : tensor<64x64xi64>, tensor<64x64xi32>) outs(%10 : tensor<64x64xi64>)
  (%in: i64, %in_5: i32) {
    %11 = arith.extsi %in_5 : i32 to i64
    %c2_i64 = arith.constant 2 : i64
    %12 = arith.muli %11, %c2_i64 : i64
    %13 = arith.addi %in, %12 : i64
    linalg.yield %13 : i64
  }

tt.make_range

tt.make_range 是由 tl.arange 下降来的，表示一个连续数组[start, end)。从 tt.make_range可以直接获取到 start(op.getStart()) 和 end(op.getEnd()) 值

%range = tt.make_range {end = 129 : i32, start = 1 : i32} : tensor<128xi32>
->
%c1_i32 = arith.constant 1 : i32
%c129_i32 = arith.constant 129 : i32
%range = linalg_ext.make_range {operandSegmentSizes = array<i32: 2, 1>} ins(%c1_i32, %c129_i32 : i32, i32) outs(%0 : tensor<128xi32>) -> tensor<128xi32>

tt.dot

tt.dot 就是矩阵乘，从 tt.dot 中使用 getA(), getB(), getC() 就能获取到 input, filter, bias ，然后直接构造 linalg.matmul 即可。

%dot =  tt.dot %input, %filter, %bias, inputPrecision = tf32 : tensor<128x64xf16> * tensor<64x64xf16> -> tensor<128x64xf32>
->
%0 = linalg.matmul ins(%input, %filter : tensor<128x64xf16>, tensor<64x64xf16>) outs(%bias : tensor<128x64xf16>) -> tensor<128x64xf16>

tt.bitcast

tt.bitcast 用于在同bit位下cast数据类型(e.g. f16->bf16)。直接下降到 arith.bitcast，若operand是tensor就下降为 linalg.map{arith.bitcast}。

%bitcast = tt.bitcast %arg0 : tensor<128xi32> -> tensor<128xf32>
->
%bitcast = linalg.map { arith.bitcast } ins(%arg0 : tensor<128xi32>) outs(%0 : tensor<128xf32>)

tt.extern_elementwise

调用额外函数(libdevice)。自定义了 linalg_ext.libdevice_call 和 `linalg_ext.scalar_libdevice_call

%0 = tt.extern_elementwise %arg0, %arg1 {libname = "a",  libpath = "b",  symbol = "__cn_vector_mul_f32_rn", pure = true} : (tensor<16x16xf32>, tensor<16x16xf32>) -> (tensor<16x16xf32>)
->
%1 = linalg_ext.libdevice_call ins(%arg0, %arg1 : tensor<16x16xf32>, tensor<16x16xf32>) outs(%0 : tensor<16x16xf32>) symbol = "__cn_vector_mul_f32_rn" -> tensor<16x16xf32>

tt.int_to_ptr / tt.ptr_to_int

tt.int_to_ptr 和 tt.ptr_to_int 分别是用来实现 int64-to-pointer 和 pointer-to-int 的，但 conversion 的每一个pattern都会使用 TypeConverter 来将 !tt.ptr 转为 int64，这两个op也就没了作用。都直接使用它们的第一个 operand 来替换 rewriter.replaceOp(op, adaptor.getOperands()[0]);。

tt.trans

tt.trans 用来对 tensor 进行转置，其 op.getOrder() 得到的值直接作为 linalg.transpose 的 permutation 参数。

%trans = tt.trans %arg0 {order=array<i32: 1, 0>} : tensor<16x32xf32> -> tensor<32x16xf32>
->
%trans = linalg.transpose ins(%arg0 : tensor<16x32xf32>) outs(%empty : tensor<32x16xf32>) permutation = [1, 0]

tt.print / tt.assert

tt.ptint 和 tt.assert 都是 debug 时用的算子，分别转为自定义的 aux.print 或 aux.scalar.print 和 linalg_ext.assert。

对于 tt.print 算子，下降时一定会产生三个 aux.scalar.print 用来打印三维 pid 信息。

tt.reduce

tt.reduce 用于 reduce 某一个维度。由于 linalg.reduce 的 init 也参与运算，所以就需要从 tt.reduce 中获得这个 init。使用 arith::getNeutralElement 去获取 tt.reduce 内进行计算的 payloadOp 的 getNeutralElement 作为 linalg.fill 的 fillVal，如果没有，那么则将 tt.reduce的第一个值抽出来单独计算作为 init。（因为reduce内的计算可能受初值的影响，所以不能简单地以0为初值）

TritonReducePattern算其中比较复杂的conversion，推荐大家阅读下，尤其是edge case的处理。

%0 = "tt.reduce" (%arg0) ({
^bb0(%arg1: i32, %arg2: i32):
  %1 = arith.subi %arg1, %arg2 : i32
  tt.reduce.return %1 : i32
}) {axis = 1 : i32} : (tensor<1x2048xi32>) -> tensor<1xi32>
->
// 由于 `arith::getNeutralElement` 没从 `arith.subi` 中获取到期望的 fillVal
// 那么则extract出reduction轴上的第一个值作为linalg.reduce的init
%extracted_slice = tensor.extract_slice %arg0[0, 0] [1, 1] [1, 1] : tensor<1x2048xi32> to tensor<1x1xi32>
%collapsed = tensor.collapse_shape %extracted_slice [[0, 1]] : tensor<1x1xi32> into tensor<1xi32>
%extracted_slice_0 = tensor.extract_slice %arg0[0, 1] [1, 2047] [1, 1] : tensor<1x2048xi32> to tensor<1x2047xi32>
%reduced = linalg.reduce ins(%extracted_slice_0 : tensor<1x2047xi32>) outs(%collapsed : tensor<1xi32>) dimensions = [1]
  (%in: i32, %init: i32) {
    %0 = arith.subi %in, %init : i32
    linalg.yield %0 : i32
  }

tt.scan

tt.scan 操作对输入序列的每个元素应用某种二元操作（如加法或乘法），并产生一个新的序列，其中每个元素是输入序列中所有前面元素的累积结果。和 tt.reduce 下降时相同，将第一个数 tensor.extract_slice 出来作为 linalg_ext.scan 的 init。最后再将 linalg_ext.scan 的结果和 init 通过 tensor.insert_slice 结合起来。

以加法为例：

  
%0 = "tt.scan" (%arg0) ({
 ^bb0(%arg1: i32, %arg2: i32):
   %1 = arith.addi %arg1, %arg2 : i32
   tt.scan.return %1 : i32
 }) {axis = 1 : i32, reverse = false} : (tensor<1x2048xi32>) -> tensor<1x2048xi32>
->
%extracted_slice = tensor.extract_slice %arg0[0, 1] [1, 2047] [1, 1] : tensor<1x2048xi32> to tensor<1x2047xi32>
%0 = tensor.empty() : tensor<1x2047xi32>
%extracted_slice_0 = tensor.extract_slice %arg0[0, 0] [1, 1] [1, 1] : tensor<1x2048xi32> to tensor<1x1xi32>
%collapsed = tensor.collapse_shape %extracted_slice_0 [[0, 1]] : tensor<1x1xi32> into tensor<1xi32>
%scanned:2 = linalg_ext.scan ins(%extracted_slice : tensor<1x2047xi32>) outs(%0, %collapsed : tensor<1x2047xi32>, tensor<1xi32>) dimensions = [1] reverse = false {
^bb0(%in: i32, %arg1: i32, %arg2: i32):
  %1 = arith.addi %in, %arg2 : i32
  linalg_ext.yield %1, %1 : i32, i32
} -> tensor<1x2047xi32>, tensor<1xi32>
%inserted_slice = tensor.insert_slice %scanned#0 into %arg0[0, 1] [1, 2047] [1, 1] : tensor<1x2047xi32> into tensor<1x2048xi32>

tt.cat

tt.cat 一般在最高维进行 concatenate，而且两个 operand 的type完全相同(td中标明了SameTypeOperands)，所以只需要用两个 tensor.insert_slice 拼接即可。第一个的tensor.insert_slice 的 offset 为0，第二个的 offset 为 operand_shape[0]。

%cat = tt.cat %lhs, %rhs : tensor<32xf32> -> tensor<64xf32>
->
%empty = tensor.empty() : tensor<64xf32>
%inserted_slice = tensor.insert_slice %lhs into %empty[0] [32] [1] : tensor<32xf32> into tensor<64xf32>
%offset = arith.constant 32 : index
%inserted_slice_1 = tensor.insert_slice %rhs into %inserted_slice[%offset] [32] [1] : tensor<32xf32> into tensor<64xf32>

tt.join

tt.join 和 tt.cat 类似，都是拼接tensor，但 join 会（在最外维）增加维度，而 cat 只（在最外维）改变DimSize不会增加维度。也下降到 tensor.insert_slice。

%join = tt.join %arg0, %arg1 : tensor<2x8xi8> -> tensor<2x8x2xi8>
->
%insert1 = tensor.insert_slice %arg0 into %empty[0, 0, 0] [2, 8, 1] [1, 1, 1] : tensor<2x8xi8> into tensor<2x8x2xi8>
%insert2 = tensor.insert_slice %arg1 into %insert1[0, 0, 1] [2, 8, 1] [1, 1, 1] : tensor<2x8xi8> into tensor<2x8x2xi8>

tt.split

tt.split 用于将一个 tensor 沿最内维 均分为两部分，要求最内维 DimSize = 2。直接下降为 tensor.extract_slice。

%0, %1 = tt.split %arg0 : tensor<2x8x2xi8> -> tensor<2x8xi8>
->
%extract1 = tensor.extract_slice %arg0[0, 0, 0] [2, 8, 1] [1, 1, 1] : tensor<2x8x2xi8> to tensor<2x8xi8>
%extract2 = tensor.extract_slice %arg0[0, 0, 1] [2, 8, 1] [1, 1, 1] : tensor<2x8x2xi8> to tensor<2x8xi8>

tt.clampf

tt.clampf 有三个参数 getX(), getMin(), getMax() ，表示将 getX() 限制在 [getMin(), getMax()] 之间的数。根据 op.getPropagateNan() 的属性下降为

- triton::PropagateNan::NONE
  arith.maxnumf + arith.minnumf (当比较值中有NaN时，直接选择另一个值作为输出)

- triton::PropagateNan::ALL
  arith.maximumf + arith.minimumf

tt.precise_sqrt / tt.precise_divf / tt.mulhiui

tt.precise_sqrt / tt.precise_divf 直接下降到 math.sqrt / math.divf， tt.mulhiui 下降到自定义的 math_ext.mulhiui。

tt.histogram

tt.histogram 是表直方图的算子，当前下降用的是比较 naive 的实现，后续应该会增加 linalg_ext 的op来承接。

summary

依然以上文 tutorials/03-matrix-multiplication.py 的例子作总结：

输入参数部分的对应如下，需要注意 tl.constexpr 的数值只是某一个(tuning config下) kernel 的编译的结果。

matmul_kernel param	tt.func blockarg
a_ptr, b_ptr, c_ptr	%arg0, %arg1, %arg2
M, N, K	%arg3, %arg4, %arg5
stride_am, stride_ak	%arg6, 1
stride_bk, stride_bn	%arg7, 1
stride_cm, stride_cn	%arg8, 1
BLOCK_SIZE_M, BLOCK_SIZE_N, BLOCK_SIZE_K	128, 64, 64
GROUP_SIZE_M	8
ACTIVATION	None

op-to-op conversion summary:

尽量在 arith, math, linalg, tensor 中找到能承接 tt.ops 到op，arith.ops, math.ops 只处理标量，如果是op操作tensor，那下降到 linalg.map{arith.ops/math.ops}。且所有 !tt.ptr 都被 TypeConverter 给转为 i64 了。

linalg_ext.atomic_rmw，反之则用 linalg_ext.gather_atomic_rmw。

ttir	linalg-on-tensor
arith.ops 标量计算	arith.ops 标量计算
arith.ops / math.ops tensor计算	linalg.map{arith.ops} / linalg.map{math.ops}
tt.load	linalg.copy(连续) / memref.load(load一个数) / linalg_ext.gather(未分析出连续)
tt.store	bufferization.materialize_to_destination(连续) / memref.store(store一个数) / linalg_ext.scatter(未分析出连续)
tt.atomic_rmw	linalg_ext.atomic_rmw(连续) / linalg_ext.gather_atomic_rmw(未分析出连续)
tt.atomic_cas	linalg_ext.atomic_cas(连续) / linalg_ext.gather_atomic_cas(未分析出连续)
tt.get_program_id x : i32	tt.get_program_id x : i32
tt.func / tt.return / tt.call	func.func, func.return, func.call
tt.broadcast	tensor.collapse_shape + linalg.broadcast
tt.splat	linalg.fill
tt.expand_dims	tensor.expand_shape
tt.addptr	linalg.map{addi}
tt.make_range	linalg_ext.make_range
tt.dot	linalg.matmul
tt.bitcast	linalg.map{bitcast}
tt.extern_elementwise	linalg_ext.libdevice_call / linalg_ext.scalar_libdevice_call
tt.int_to_ptr / tt.ptr_to_int	直接使用第一个 operand 替换使用
tt.trans	linalg.transpose
tt.print	aux.print / aux.scalar.print
tt.assert	linalg_ext.assert
tt.reduce	linalg.reduce
tt.scan	linalg_ext.scan
tt.cat	tensor.insert_slice
tt.join / tt.split	tensor.insert_slice + tensor.insert_slice
tt.clampf	arith.maximumf(arith.maxnumf) + arith.minimumf(arith.minnumf)
tt.precise_sqrt / tt.precise_divf / tt.mulhiui	math.sqrt / math.divf / math_ext.mulhiui
tt.histogram	比较 naive 的拼接实现，后续会改为 linalg_ext.histogram

代码中构造 tensor.empty 作为输出时，很多都是使用

  
Value init = rewriter.create<tensor::EmptyOp>(loc, resultTy.getShape(),
                                              resultTy.getElementType());

但这都要求 resultTy 是 static shape 的 RankedTensorType，应该都改用 lib/Dialect/Utils/ShapeUtils.cpp 中的 getDim 函数，不然遇见 dynamic shape 就会 coredump.

  
auto initDims = triton::getDims(rewriter, loc, resultVal);
Value init =
rewriter.create<tensor::EmptyOp>(loc, initDims, resultTy.getElementType());

Pipeline

pipeline 的定义在下面的文件，从中可以看到很多 pass 都是下降过程中的 conversion pass。

  
lib/Pipelines/Pipelines.cpp

此外，还有一些非 mlir 官方的 pass 值得关注：

WrapFuncBodyWithSingleBlockPass: 当 funcOp 中有多个 block(一般含有 BranchOpInterface 的op时会有多个 block)，创建一个 scf.execute_region 将所有 block 包起来，方便后序inline。
CanonicalizeTritonPass: 为了方便后序 conversion，将 op canoncialize 成等效的形式。
PointerStrengthReductionPass: 支持跨block(BranchOpInterface和RegionBranchOpInterface)的ptr分析。
ExtractLikeMoveBackwardPass: extractOp向前移动，减少计算量。(add+extract -> extract+add)
ArithCanonicalizerPass: 将一些 arith op 转为等效的计算形式；规范化存在nan时的计算图。

这些pass的测试都在 test/Dialect/Triton/ 下

结语

感谢 cambricon/triton-linalg 团队优秀的工作，衷心希望社区多一些基于 mlir 的开源代码。

才疏学浅，只能以当下的见识为大家分享该项目的工作，欢迎大家指出问题～

Triton Linalg